题目内容
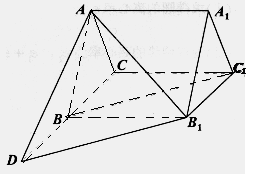
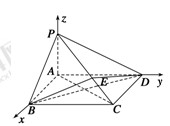
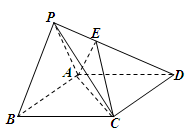
如图所示,在四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,点E在线段PC上,PC⊥平面BDE.
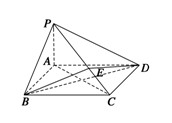
(1) 证明:BD⊥平面PAC;
(2) 若PA=1,AD=2,求二面角B-PC-A的正切值.

(1) 证明:BD⊥平面PAC;
(2) 若PA=1,AD=2,求二面角B-PC-A的正切值.
(1)见解析;(2)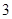 .
.
 .
.试题分析:(1)先利用直线与平面垂直的性质定理,得到
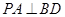 和
和 ,因为
,因为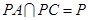 ,所以利用直线与平面垂直的判定定理可知,
,所以利用直线与平面垂直的判定定理可知,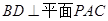 ;(2)首先分别以射线
;(2)首先分别以射线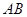 ,
,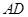 ,
,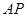 为
为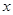 轴,
轴,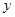 轴,
轴,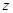 轴的正半轴建立空间直角坐标系
轴的正半轴建立空间直角坐标系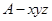 ,由直线与平面垂直的性质定理得到
,由直线与平面垂直的性质定理得到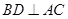 ,那么矩形
,那么矩形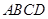 为正方形,由此可知此正方形的边的长度,根据坐标系表示四棱锥出各个顶点的坐标,分别求出平面
为正方形,由此可知此正方形的边的长度,根据坐标系表示四棱锥出各个顶点的坐标,分别求出平面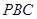 和平面
和平面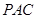 的法向量的坐标,根据二面角与其法向量夹角的关系,求得二面角的余弦值,再由同角三角函数的基本关系得到所求二面角的正切值.
的法向量的坐标,根据二面角与其法向量夹角的关系,求得二面角的余弦值,再由同角三角函数的基本关系得到所求二面角的正切值.试题解析:(1)证明 ∵
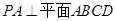 ,
,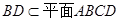 ,∴
,∴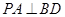 .2分
.2分同理由
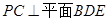 ,可证得
,可证得 .
.又
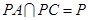 ,∴
,∴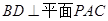 . 4分
. 4分(2)如图,分别以射线
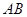 ,
,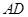 ,
,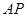 为
为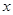 轴,
轴,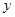 轴,
轴,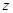 轴的正半轴建立空间直角坐标系
轴的正半轴建立空间直角坐标系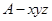 .
.
由(1)知
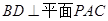 ,又
,又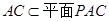 , ∴
, ∴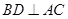 .
.故矩形
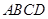 为正方形,∴
为正方形,∴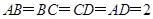 . 6分
. 6分∴
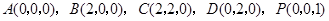 .
.∴
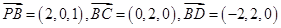 .
.设平面
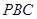 的一个法向量为
的一个法向量为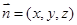 ,则
,则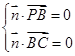 ,即
,即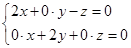 ,
,∴
 ,取
,取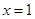 ,得
,得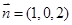 .
.∵
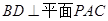 ,∴
,∴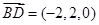 为平面
为平面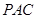 的一个法向量.10分
的一个法向量.10分所以
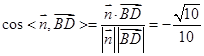 . 11分
. 11分设二面角
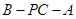 的平面角为
的平面角为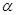 ,由图知
,由图知 ,
,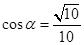 ,所以
,所以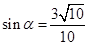 .
.∴ 所以
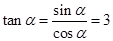 ,即二面角
,即二面角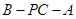 的正切值为
的正切值为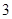 . 12分
. 12分
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
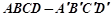 中,点
中,点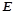 为棱
为棱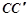 上任意一点,
上任意一点,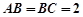 ,
,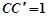 .
.

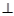 平面
平面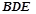 ;
;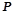 为棱
为棱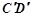 的中点,点
的中点,点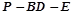 的余弦值.
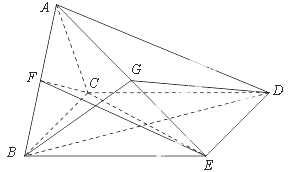
的余弦值.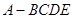 中,
中,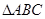 是正三角形,四边形
是正三角形,四边形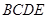 是矩形,且平面
是矩形,且平面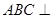 平面
平面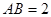 ,
,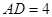 .
.
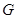 是
是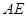 的中点,求证:
的中点,求证: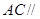 平面
平面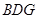 ;
;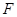 在线段
在线段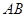 上什么位置时,二面角
上什么位置时,二面角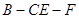 的余弦值为
的余弦值为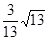 .
.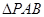 为边长为2的正三角形,底面ABCD为菱形,且平面PAB⊥平面ABCD,
为边长为2的正三角形,底面ABCD为菱形,且平面PAB⊥平面ABCD,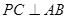 ,E为PD点上一点,满足
,E为PD点上一点,满足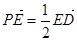
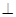 平面ABCD;
平面ABCD;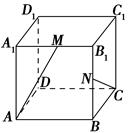
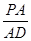 多大时,AM⊥平面PDB可能成立?
多大时,AM⊥平面PDB可能成立?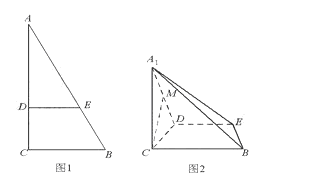
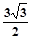 ,D是CB延长线上一点,且BD=BC.
,D是CB延长线上一点,且BD=BC.