题目内容
16.在△ABC中,角A,B,C对应的边分别为a,b,c,若b-acosB=acosC-c,则△ABC的形状是( )| A. | 等腰三角形 | B. | 等边三角形 | C. | 直角三角形 | D. | 等腰直角三角形 |
分析 利用正弦定理,三角形内角和定理,三角函数恒等变换的应用化简已知可得cosA(sinC+sinB)=0,可得cosA=0,解得三角形为直角三角形.
解答 解:在△ABC中,b-acosB=acosC-c,
由正弦定理得:sinB-sinAcosB=sinAcosC-sinC,
即:sinAcosC+cosAsinC-sinAcosB=sinAcosC-sinC,
cosAsinC-sinAcosB=-sinC=-sinAcosB-cosAsinB,
整理得:cosA(sinC+sinB)=0,sinC+sinB>0,
∴cosA=0,
∴A=$\frac{π}{2}$.
故选:C.
点评 本题主要考查了正弦定理,三角形内角和定理,三角函数恒等变换的应用在解三角形中的应用,考查了分类讨论思想,属于中档题.

练习册系列答案
相关题目
6.若x∈{1,2,3},y∈{3,6},则xy的不同值有( )
| A. | 3个 | B. | 5个 | C. | 6个 | D. | 9个 |
7.有一个综艺节目,选手面对1~8号8扇大门,依次按响门上的门铃,门铃会播放一段音乐,选手需正确回答出这首歌的名字,方可获得该扇门对应的家庭梦想基金,某机构随机抽取50个参与节目的选手的年龄作为样本进行分析研究,由此得到如下频数分布表(所有参与节目的选手年龄都在[5,65)内).
(Ⅰ)在表中作出这些数据的频率分布直方图;
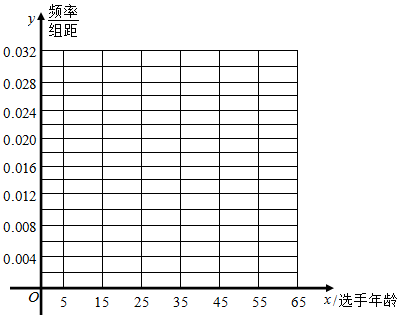
(Ⅱ)若将频率视为概率,从参与节目的选手中随机抽取3位(看作有放回地抽取),求年龄在[35,45)内的选手人数X的分布列、数学期望.
| 选手年龄 | [5,15) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) |
| 频数 | 2 | 12 | 16 | 10 | 7 | 3 |

(Ⅱ)若将频率视为概率,从参与节目的选手中随机抽取3位(看作有放回地抽取),求年龄在[35,45)内的选手人数X的分布列、数学期望.
5.数列{an}的通项an=n2cos$\frac{2nπ}{3}$,其前n项和为Sn,则S60为( )
| A. | 1840 | B. | 1860 | C. | 1880 | D. | 2010 |
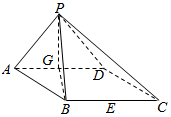 如图,在四棱锥P-ABCD中,底面ABCD是边长为2的菱形,且∠DAB=60°,侧面PAD为正三角形,其所在平面垂直于底面ABCD,G为AD边的中点,E为BC所在直线上的一点
如图,在四棱锥P-ABCD中,底面ABCD是边长为2的菱形,且∠DAB=60°,侧面PAD为正三角形,其所在平面垂直于底面ABCD,G为AD边的中点,E为BC所在直线上的一点