题目内容
9.对每个x,y是y1=2x,y2=x+2,y3=-$\frac{3}{2}$x+12三个值中的最小值,则当x变化时,函数y的最大值是6.分析 利用几何画板可得图象,联立$\left\{\begin{array}{l}{y=x+2}\\{y=-\frac{3}{2}x+12}\end{array}\right.$,解出即可得出.
解答  解:如图所示利用几何画板可得:
解:如图所示利用几何画板可得:
联立$\left\{\begin{array}{l}{y=x+2}\\{y=-\frac{3}{2}x+12}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=4}\\{y=6}\end{array}\right.$.
可知:当x变化时,函数y的最大值是6.
故答案为:6.
点评 本题考查了直线的方程、数的大小比较,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
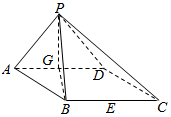 如图,在四棱锥P-ABCD中,底面ABCD是边长为2的菱形,且∠DAB=60°,侧面PAD为正三角形,其所在平面垂直于底面ABCD,G为AD边的中点,E为BC所在直线上的一点
如图,在四棱锥P-ABCD中,底面ABCD是边长为2的菱形,且∠DAB=60°,侧面PAD为正三角形,其所在平面垂直于底面ABCD,G为AD边的中点,E为BC所在直线上的一点