题目内容
3.已知幂函数$f(x)={x^{{m^2}-2m-3}}(m∈Z)$的图象关于y轴对称,并且f(x)在第一象限是单调递减函数.(1)求m的值;
(2)解不等式f(1-2x)≥f(2).
分析 利用幂函数的奇偶性和单调性即可求出.
解答 解:因为幂函数f(x)=x${\;}^{{m}^{2}-2m-3}$(m∈Z)的图象关于y轴对称,
所以函数f(x)是偶函数,
∴m2-2m-3为偶数,
∴m2-2m为奇函数,
故m=1;
(2)∵f(x)在第一象限是单调递减函数,f(x)为偶函数,
又f(1-2x)≥f(2),
∴|1-2x|≤2,
解得:-$\frac{1}{2}$≤x$≤\frac{3}{2}$.
点评 熟练掌握幂函数的奇偶性和单调性是解题的关键

练习册系列答案
相关题目
16.复数(3-4i)i(其中i为虚数单位)在复平面内对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
12.“a=-3”是“函数y=x2+2(a-1)x+2在区间(-∞,4]上单调递减”的( )
| A. | 充分非必要条件 | B. | 必要非充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
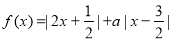 .
.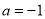 时,解不等式
时,解不等式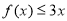 ;
;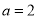 时,若关于
时,若关于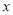 的不等式
的不等式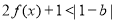 的解集为空集,求实数
的解集为空集,求实数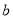 的取值范围.
的取值范围.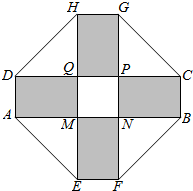 2010年上海世博会某国要建一座八边形的展馆区,它的主体造型的平面图是由两个相同的矩形ABCD和EFGH构成的面积为200m2的十字型地域,计划在正方形MNPQ上建一座“观景花坛”,造价为4200元/m2,在四个相同的矩形上(图中阴影部分)铺花岗岩地坪,造价为210元/m2,再在四个空角(如△DQH等)上铺草坪,造价为80元/m2.设AD长为xm,DQ长为ym.
2010年上海世博会某国要建一座八边形的展馆区,它的主体造型的平面图是由两个相同的矩形ABCD和EFGH构成的面积为200m2的十字型地域,计划在正方形MNPQ上建一座“观景花坛”,造价为4200元/m2,在四个相同的矩形上(图中阴影部分)铺花岗岩地坪,造价为210元/m2,再在四个空角(如△DQH等)上铺草坪,造价为80元/m2.设AD长为xm,DQ长为ym.