题目内容
已知y=ax (a>0且a≠1)是定义在R上的单调递减函数,记a的所有可能取值构成集合A;P(x,y)是椭圆
+
=1上一动点,点P1(x1,y1)与点P关于直线y=x+1对称,记
的所有可能取值构成集合B.若随机地从集合A,B中分别抽出一个元素λ1,λ2,则λ1>λ2的概率是 .
| x2 |
| 16 |
| y2 |
| 9 |
| y1-1 |
| 4 |
考点:几何概型
专题:概率与统计
分析:根据指数函数的性质以及直线和圆锥曲线的位置关系求出集合A,B,然后根据几何概型的概率公式即可得到结论.
解答:
 解:∵y=ax (a>0且a≠1)是定义在R上的单调递减函数,∴0<a<1,
解:∵y=ax (a>0且a≠1)是定义在R上的单调递减函数,∴0<a<1,
∴A={a|0<a<1}.
P1(x1,y1)关于直线y=x+1的对称点为P(y1-1,x1+1),
P是椭圆
+
=l上一动点,
∴-4≤y1-1≤4,
即-1≤
≤1,
设b=
,则-1≤b≤1,
∴B={b|-1≤b≤1}.
∴随机的从集合A,B中分别抽取一个元素λ1,λ2,则λ1>λ2等价为
,
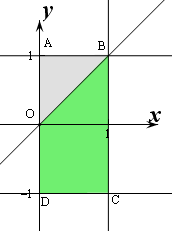
则对应的图象如图:
则λ1>λ2的概率是
,
故答案为:
 解:∵y=ax (a>0且a≠1)是定义在R上的单调递减函数,∴0<a<1,
解:∵y=ax (a>0且a≠1)是定义在R上的单调递减函数,∴0<a<1,∴A={a|0<a<1}.
P1(x1,y1)关于直线y=x+1的对称点为P(y1-1,x1+1),
P是椭圆
| x2 |
| 16 |
| y2 |
| 9 |
∴-4≤y1-1≤4,
即-1≤
| y1-1 |
| 4 |
设b=
| y1-1 |
| 4 |
∴B={b|-1≤b≤1}.
∴随机的从集合A,B中分别抽取一个元素λ1,λ2,则λ1>λ2等价为
|
则对应的图象如图:
则λ1>λ2的概率是
| 3 |
| 4 |
故答案为:
| 3 |
| 4 |
点评:本题主要考查几何概型的概率计算,利用直线和圆锥曲线的位置关系求出集合A,B是解决本题的关键.综合性较强,难度非常大.

练习册系列答案
相关题目
已知直线l与过点M(-
,
)、N(
,-
)的直线垂直,则直线l的倾斜角是( )
| 3 |
| 2 |
| 2 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
已知p:|2x-3|<1,q:x(x-3)<0,则p是q的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |