题目内容
16.设二次函数f(x)=-$\frac{1}{2}$x2+m图象的顶点为C,与x轴的交点分别为A、B.若△ABC的面积为8$\sqrt{2}$.(1)求m的值;
(2)求函数f(x)在区间[-1,2]上的最大值与最小值.
分析 (1)可令f(x)=0,从而可以解出x=$±\sqrt{2m}$,这样可以求出AB=$2\sqrt{2m}$,而OC=m,从而根据△ABC的面积为8$\sqrt{2}$便可求出m=4;
(2)写出$f(x)=-\frac{1}{2}{x}^{2}+4$,从而可以看出x分别取0,2时,f(x)在区间[-1,2]上分别取到最大、最小值,并且可求出该最大、最小值.
解答 解:(1)如图,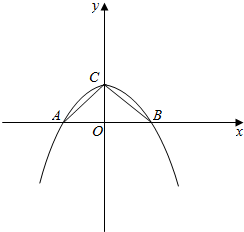
令f(x)=0得,x=$±\sqrt{2m}$,OC=m;
∴${S}_{△ABC}=\frac{1}{2}•(2\sqrt{2m})•m=8\sqrt{2}$;
∴m=4;
(2)$f(x)=-\frac{1}{2}{x}^{2}+4$;
∵x∈[-1,2];
∴x=0时,f(x)取最大值4,x=2时,f(x)取最小值2;
∴f(x)在区间[-1,2]上的最大值为4,最小值为2.
点评 考查二次函数的图象,三角形的面积公式,二次函数在闭区间上的最大、最小值的求法,以及数形结合解题的方法.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
6.函数y=-cos2x+$\sqrt{3}$cosx+$\frac{5}{4}$,则( )
| A. | 最大值是$\frac{5}{4}$,最小值是1 | B. | 最大值是1,最小值是$\frac{1}{4}$-$\sqrt{3}$ | ||
| C. | 最大值是2,最小值是$\frac{1}{4}$-$\sqrt{3}$ | D. | 最大值是2,最小值是$\frac{5}{4}$ |
4.若(2-x)2013=a0+a1x+a2x2+…+a2013x2013,则$\frac{{a}_{0}+{a}_{2}+{a}_{4}+…{+a}_{2012}}{{a}_{1}+{a}_{3}+{a}_{5}+…+{a}_{2013}}$=( )
| A. | $\frac{{3}^{2013}+1}{{3}^{2013}-1}$ | B. | -$\frac{{3}^{2013}+1}{{3}^{2013}-1}$ | ||
| C. | $\frac{{3}^{2012}+1}{{3}^{2012}-1}$ | D. | -$\frac{{3}^{2012}+1}{{3}^{2012}-1}$ |
1.若θ为第二象限角,那么sin(cos2θ)•cos(sin2θ)的值为( )
| A. | 正值 | B. | 负值 | C. | 零 | D. | 以上都有可能 |
18.等比数列{an}的前4项和为4,前12项和为28,则它的前8项和是( )
| A. | -8 | B. | 12 | C. | -8或12 | D. | 8 |
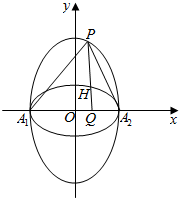 若两个椭圆的离心率相等,则称它们为“相似椭圆”.如图,在直角坐标系xOy中,已知椭圆C1:$\frac{{x}^{2}}{6}$+$\frac{{y}^{2}}{3}$=1,A1,A2分别为椭圆C1的左右顶点,椭圆C2以线段A1A2为短轴且与椭圆C1为“相似椭圆”
若两个椭圆的离心率相等,则称它们为“相似椭圆”.如图,在直角坐标系xOy中,已知椭圆C1:$\frac{{x}^{2}}{6}$+$\frac{{y}^{2}}{3}$=1,A1,A2分别为椭圆C1的左右顶点,椭圆C2以线段A1A2为短轴且与椭圆C1为“相似椭圆”