题目内容
若函数f(x)=ln(x2+ax-1)是偶函数,则函数的定义域是 .
考点:函数的定义域及其求法
专题:计算题,函数的性质及应用,不等式的解法及应用
分析:由偶函数的定义f(-x)=f(x)即可求得a的值,再由x2-1>0,解得即可.
解答:
解:∵f(x)=ln(x2+ax-1)是偶函数,
∴f(-x)=f(x).
即ln[(-x)2-ax-1]=ln(x2+ax-1),
即有(-x)2-ax-1=x2+ax-1,
∴2ax=0,又x不恒为0,
∴a=0.
则f(x)=ln(x2-1),
由x2-1>0,解得,x>1或x<-1.
则定义域为:(-∞,-1)∪(1,+∞).
故答案为:(-∞,-1)∪(1,+∞).
∴f(-x)=f(x).
即ln[(-x)2-ax-1]=ln(x2+ax-1),
即有(-x)2-ax-1=x2+ax-1,
∴2ax=0,又x不恒为0,
∴a=0.
则f(x)=ln(x2-1),
由x2-1>0,解得,x>1或x<-1.
则定义域为:(-∞,-1)∪(1,+∞).
故答案为:(-∞,-1)∪(1,+∞).
点评:本题考查函数奇偶性的性质,以及函数的定义域,注意对数的真数必须大于0,同时利用偶函数的定义是关键,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
四个小动物换座位,开始是鼠、猴、兔、猫分别坐1、2、3、4号位上(如图),第一次前后排动物互换座位,第二次左右列动物互换座位,…这样交替进行下去,那么第202次互换座位后,小兔坐在第( )号座位上
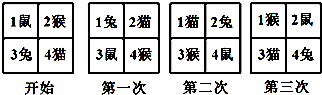

| A、1 | B、2 | C、3 | D、4 |
已知全集U={x∈N*|x<6},A={1,3},B={3,5},则∁U(A∪B)等于( )
| A、{1,4} |
| B、{1,5} |
| C、{2,4} |
| D、{2,5} |
设z1,z2为复数,则下列四个结论中正确的是( )
| A、若z12+z22>0,则z12>-z22 | ||
| B、若z12+z22=0,则z1=z2=0 | ||
C、|z1-z2|=
| ||
D、z1-
|
设全集U=R,集合A={x|x<0},B={x|-1<x<3},则A∩B=( )
| A、{x|-1<x<0} |
| B、{x|0<x<3} |
| C、{x|x<0} |
| D、{x|x<3} |