题目内容

20．已知{an}是公差不为0的等差数列，Sn是其前n项和，若a2a3=a4a5，S4=27，则a1的值是$\frac{135}{8}$．

分析 设等差数列{an}的公差为d（d≠0），由等差数列的通项公式、前n项和公式列出方程组，求出a1的值．

解答 解：设等差数列{an}的公差为d（d≠0），
∵a2a3=a4a5，S4=27，
∴$\left\{\begin{array}{l}{（{a}_{1}+d）（{a}_{1}+2d）=（{a}_{1}+3d）（{a}_{1}+4d）}\\{4{a}_{1}+\frac{4×3}{2}d=27}\end{array}\right.$，
解得：a1=$\frac{135}{8}$，
故答案为：$\frac{135}{8}$．

点评 本题考查等差数列的通项公式、前n项和公式，以及方程思想，考查化简、计算能力．

练习册系列答案
相关题目
10．抛物线y2=4x上一点A到它焦点F的距离为4，则直线AF的斜率为$±\sqrt{3}$．
11．已知曲线C1的参数方程为$\left\{\begin{array}{l}x=acosθ\\ y=bsinθ\end{array}\right.$（a＞b＞0，θ为参数），以坐标原点O为极点，x轴的正半轴为极轴建立极坐标系，曲线C2的极坐标方程为ρ=r（r＞0）．
（1）求曲线C1的普通方程与曲线C2的直角坐标方程，并讨论两曲线公共点的个数；
（2）若b＜r＜a，求由两曲线C1与C2交点围成的四边形面积的最大值．
8．定义域为R的偶函数f（x）满足?x∈R，有f（x+2）=f（x）-f（1），且当x∈[2，3]时，f（x）=-2x2+12x-18，若函数y=f（x）-loga（x+1）恰有三个零点，则a的取值范围是（　　）
A．（0，$\frac{\sqrt{5}}{5}$）B．（0，$\frac{\sqrt{3}}{3}$）C．（$\frac{\sqrt{5}}{5}$，$\frac{\sqrt{3}}{3}$）D．（$\frac{\sqrt{6}}{6}$，$\frac{\sqrt{5}}{5}$）
15．已知集合A={0，3，4}，B={-1，0，2，3}，则A∩B={0，3}．
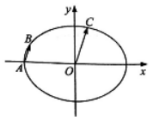5．如图，在平面直角坐标系xOy中，已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率为$\frac{2}{3}$，C为椭圆上位于第一象限内的一点．
（1）若点C的坐标为（2，$\frac{5}{3}$），求a，b的值；
（2）设A为椭圆的左顶点，B为椭圆上一点，且$\overrightarrow{AB}$=$\frac{1}{2}$$\overrightarrow{OC}$，求直线AB的斜率．
12．已知a=20.1，$b={（{\frac{1}{2}}）^{-0.4}}$，c=2log72，则a，b，c的大小关系为（　　）
A．c＜a＜bB．c＜b＜aC．b＜a＜cD．b＜c＜a
9．将函数f（x）=cos（2x-$\frac{π}{3}$）的图象向左平移$\frac{π}{6}$个单位，所得图象对应的函数解析式为y=cos2x．
13．已知e是自然对数的底数，实数a是常数，函数f（x）=ex-ax-1的定义域为（0，+∞）．
（1）设a=e，求函数f（x）在切点（1，f（1））处的切线方程；
（2）判断函数f（x）的单调性；
（3）设g（x）=ln（ex+$\frac{e}{3}$x3-1）-lnx，若?x＞0，f（g（x））＜f（x），求a的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网