题目内容
5.若实数x,y满足$\left\{\begin{array}{l}{x+2y-4≤0}\\{x-y-1≤0}\\{x≥1}\end{array}\right.$,则x2+y2的最大值为( )| A. | 1 | B. | 4 | C. | 6 | D. | 5 |
分析 作出平面区域,则x2+y2表示平面区域内的点到原点的最大距离的平方.
解答 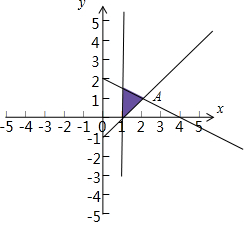 解:作出实数x,y满足$\left\{\begin{array}{l}{x+2y-4≤0}\\{x-y-1≤0}\\{x≥1}\end{array}\right.$的平面区域如图:
解:作出实数x,y满足$\left\{\begin{array}{l}{x+2y-4≤0}\\{x-y-1≤0}\\{x≥1}\end{array}\right.$的平面区域如图:
解方程组$\left\{\begin{array}{l}{x+2y-4=0}\\{x-y-1=0}\end{array}\right.$得,∴A(2,1).
由题意可知A到原点的距离的平方最大,
∴|OA|2=22+12=5.
∴x2+y2的最大值是5.
故选:D.
点评 本题考查了简单的线性规划,弄清x2+y2的几何意义是解题关键,属于基础题.

练习册系列答案
相关题目
16.已知i是虚数单位,$\overline z$是复数z的共轭复数,$\overline z+|z|•i=1+2i$,则z的虚部为( )
| A. | $-\frac{3}{4}$ | B. | $\frac{3}{4}$ | C. | $-\frac{3}{4}i$ | D. | $\frac{3}{4}i$ |
13.将正奇数按如图所示的规律排列,则第21行从左向右的第5个数为( )


| A. | 731 | B. | 809 | C. | 852 | D. | 891 |
20.教学大楼共有五层,每层均有两个楼梯,由一层到五层的走法有( )
| A. | 10种 | B. | 32种 | C. | 25种 | D. | 16种 |