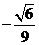题目内容
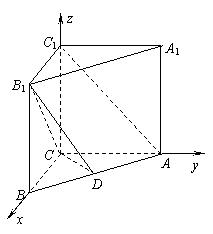
如图,直三棱柱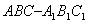 中,
中,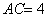 ,
,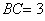 ,
, ,
,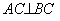 ,点
,点 在线段
在线段 上.
上.
(Ⅰ)证明 ;
;
(Ⅱ)若 是
是 中点,证明
中点,证明 ∥平面
∥平面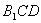 ;
;
(Ⅲ)当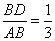 时,求二面角
时,求二面角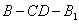 的余弦值.
的余弦值.

证明:(Ⅰ)如图,以C为原点建立空间直角坐标系C-xyz.则 (3, 0, 0),
(3, 0, 0),
 (0, 4, 0),
(0, 4, 0), (0, 4, 4),
(0, 4, 4),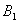 (3, 0, 4),
(3, 0, 4),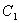 (0, 4, 4).
(0, 4, 4).
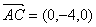
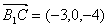
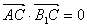 所以
所以
(Ⅱ)解法一:
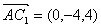
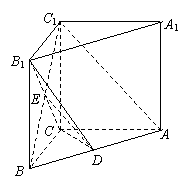 设平面B1 CD的法向量为
设平面B1 CD的法向量为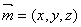 ,
,
由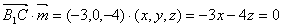
且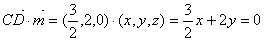 ,
,
令x = 4得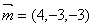 ,
,
所以 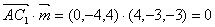
又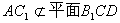 所以 AC1∥平面B1CD;
所以 AC1∥平面B1CD;
解法二:证明:连结BC1,交B1C于E,DE.
因为 直三棱柱ABC-A1B1C1,D是AB中点,
所以侧面B B1C1C为矩形,DE为△ABC1的中位线,
所以 DE// AC1.
因为 DE 平面B1CD, AC1
平面B1CD, AC1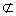 平面B1CD,
平面B1CD,
所以 AC1∥平面B1CD.
(Ⅲ)解:由(Ⅰ)知AC⊥BC,
设D (a, b, 0)(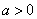 ,
,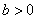 ),
),
因为 点D在线段AB上,且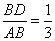 , 即
, 即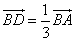 .
.
所以 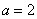 ,
,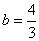 ,
,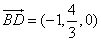 .
.
所以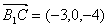 ,
,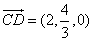 .
.
平面BCD的法向量为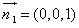 .
.
设平面B1 CD的法向量为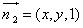 ,
,
由 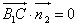 ,
,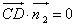 , 得
, 得 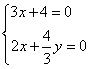 ,
,
所以 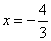 ,
,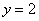 ,
,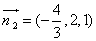 .
.
设二面角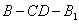 的大小为
的大小为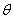 ,
,
所以 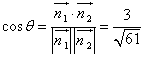 .
.
所以 二面角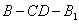 的余弦值为
的余弦值为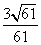 .
.

练习册系列答案
相关题目
 的准线与直线
的准线与直线 之间的距离为3,则该抛物线的方程为 .
之间的距离为3,则该抛物线的方程为 .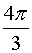 ,则圆锥的体积是________
,则圆锥的体积是________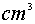 .
. 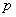 为假命题,命题
为假命题,命题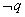 为假命题,则命题“
为假命题,则命题“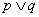 ”为假命题;
”为假命题;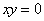 ,则
,则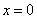 或
或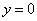 ”的否命题为“若
”的否命题为“若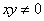 ,则
,则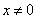 或
或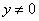 ”;
”;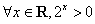 ”的否定是“
”的否定是“ 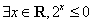 ”.则以上结论正确的个数为
”.则以上结论正确的个数为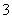 B.
B. C.
C. D.
D.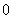
 是圆的两条弦,过点
是圆的两条弦,过点 作
作 的平行线与圆交于点
的平行线与圆交于点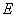 ,与
,与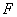 ,
, ,
, ,
, ,则线段
,则线段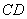 的长为 .
的长为 .
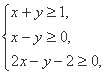 则目标函数z=2x+y的最小值为
则目标函数z=2x+y的最小值为
 B=_________.
B=_________.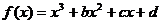 的大致图像,
的大致图像, 则
则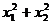 等于( )
等于( )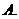
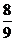
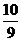
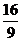
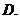
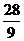
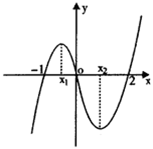
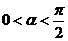 ,
,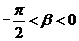 ,
,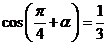 ,
,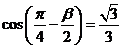 ,则
,则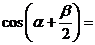 ( ).
( ).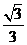 B.
B.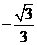 C.
C.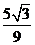 D.
D.