题目内容
已知f(x)是以5为周期的奇函数,f(-3)=-4且cosα=
,则f(4cos2α)= .
| 1 |
| 2 |
考点:函数的周期性,函数的值
专题:函数的性质及应用
分析:由已知得f(4cos2α)═f[4×(2cos2α-1)]=f(-2)=f(3)=-f(-3)=4.
解答:
解:∵f(x)是以5为周期的奇函数,f(-3)=-4且cosα=
,
∴f(4cos2α)═f[4×(2cos2α-1)]
=f(-2)
=f(3)
=-f(-3)=4.
故答案为:4.
| 1 |
| 2 |
∴f(4cos2α)═f[4×(2cos2α-1)]
=f(-2)
=f(3)
=-f(-3)=4.
故答案为:4.
点评:本题考查函数值的求法,是基础题,解题时要认真审题,注意函数性质的合理运用.

练习册系列答案
相关题目
已知曲线f(x)=xn+1(n∈N*)与直线x=1交于点P,若设曲线y=f(x)在点P处的切线与x轴交点的横坐标为xn,则log2015x1+log2015x2+…+log2015x2014的值为 .
执行如图的程序框图,输出的结果为( )
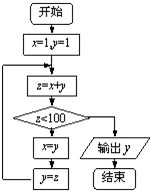

| A、55 | B、89 |
| C、144 | D、233 |
命题“如果实数x能被2整除,则x是偶数”的否命题是( )
| A、如果实数x不能被2整除,则x是偶数 |
| B、如果实数x能被2整除,则x不是偶数 |
| C、如果实数x不能被2整除,则x不是偶数 |
| D、存在一个能被2整除的数,它不是偶数 |