题目内容
11. 40名高三学生某次数学考试成绩(单位:分)的频率分布直方图如下:
40名高三学生某次数学考试成绩(单位:分)的频率分布直方图如下:(Ⅰ)求频率分布直方图中x的值;
(Ⅱ)分别求出成绩落在(130,140]与(140,150]中的学生人数;
(Ⅲ)从成绩落在(130,150]中的学生中任选2人,记成绩落在(140,150]中的人数为X,求X的分布列与数学期望.
分析 (Ⅰ)由频率分布直方图中小矩形面积之和为1,能求出x.
(Ⅱ)先求出成绩落在(130,140]与(140,150]中的频率,由此能求出成绩落在(130,140]与(140,150]中的学生人数.
(Ⅲ)成绩落在(130,150]中的学生人数为6人,从中任选2人,成绩落在(140,150]中的人数X的可能取值为0,1,2,分别求出相应的概率,由此能求出X的分布列和EX.
解答 解:(Ⅰ)由频率分布直方图,得:
(0.005×2+2x+0.015+0.020+0.035)×10=1,
解得x=0.01.
(Ⅱ)成绩落在(130,140]与(140,150]中的频率分别为:
0.01×10=0.1和0.005×10=0.05,
∴成绩落在(130,140]与(140,150]中的学生人数分别为:
0.1×40=4人和0.05×40=2人.
(Ⅲ)成绩落在(130,150]中的学生人数为:4+2=6人,
从中任选2人,成绩落在(140,150]中的人数X的可能取值为0,1,2,
P(X=0)=$\frac{{C}_{4}^{2}}{{C}_{6}^{2}}$=$\frac{2}{5}$,
P(X=1)=$\frac{{C}_{2}^{1}{C}_{4}^{1}}{{C}_{6}^{2}}$=$\frac{8}{15}$,
P(X=2)=$\frac{{C}_{2}^{2}}{{C}_{6}^{2}}$=$\frac{1}{15}$,
∴X的分布列为:
| X | 0 | 1 | 2 |
| P | $\frac{2}{5}$ | $\frac{8}{15}$ | $\frac{1}{15}$ |
点评 本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,注意排列组合知识的合理运用.

练习册系列答案
相关题目
2.若复数z满足zi=1+2i,则复数z的共轭复数$\overline{z}$=( )
| A. | -2-i | B. | -2+i | C. | 2-i | D. | 2+i |
16.设P={x|2x<16},Q={x|x2<4},则( )
| A. | P⊆Q | B. | Q⊆P | C. | P⊆∁RQ | D. | Q⊆∁RP |
20.设过椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0,c=$\sqrt{{a}^{2}-{b}^{2}}$)的左焦点与上顶点的直线为l,若坐标原点O到直线l的距离为$\frac{c}{2}$,则椭圆的离心率为( )
| A. | $\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{1}{2}$ | D. | $\frac{\sqrt{3}}{3}$ |
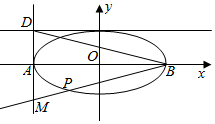 如图,椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左、右顶点分别为A,B,焦距为2$\sqrt{2}$,直线x=-a与y=b交于点D,且|BD|=3$\sqrt{2}$,过点B作直线l交直线x=-a于点M,交椭圆于另一点P.
如图,椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的左、右顶点分别为A,B,焦距为2$\sqrt{2}$,直线x=-a与y=b交于点D,且|BD|=3$\sqrt{2}$,过点B作直线l交直线x=-a于点M,交椭圆于另一点P.