Question

在矩形ABCD中，

AE

=

1

2

AB

，

BF

=

FC

，设

AB

=（a，0），

AD

=（0，b），当

EF

⊥

DE

时，求得

|a|

|b|

的值为（　　）

• A、3
• B、2
• C、

  3

• D、

  2

Answer 1

考点：平面向量数量积的运算,向量加减混合运算及其几何意义

专题：平面向量及应用

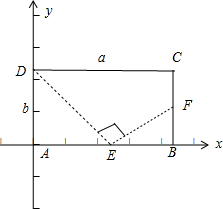
分析：由题意可得，AB=|a|，BC=|b|．以AB所在的直线为x轴，以AD所在的直线为y轴，建立平面直角坐标系，可得A（0，0）、B（a，0）、D（0，b）、E（

a

2

，0）、F（a，

b

2

）．由

EF

⊥

DE

时，可得

EF

•

ED

=0，求得 a²=2b²，可得

|a|

|b|

=的值．

解答： 解：在矩形ABCD中，∵

AE

=

1

2

AB

，

BF

=

FC

，∴E为AB的中点，F为BC的中点．
又

AB

=（a，0），

AD

=（0，b），∴AB=|a|，BC=|b|．
以AB所在的直线为x轴，以AD所在的直线为y轴，建立平面直角坐标系，
可得A（0，0）、B（a，0）、D（0，b）、E（

a

2

，0）、F（a，

b

2

）．
当

EF

⊥

DE

时，由

EF

•

ED

=（

a

2

，

b

2

）•（-

a

2

，b）=-

a2

4

+

b2

2

=0，可得 a²=2b² ，∴

|a|

|b|

=

2

，
故选：D．

点评：本题主要考查两个向量的加减法的法则，以及其几何意义，两个向量垂直的性质，两个向量数量积公式，属于基础题．