题目内容
等差数列{an}、{bn}满足
=
（n∈N*），且前n项和分别为An、Bn，则
的值为 ．
| an |
| bn |
| 3n+2 |
| 4n+3 |
| A5 |
| B5 |
考点：等差数列的性质
专题：等差数列与等比数列
分析：在等差数列中，由
=
结合已知求得答案．
| A5 |
| B5 |
| 5a3 |
| 5b3 |
解答：
解：∵{an}、{bn}为等差数列，且前n项和分别为An、Bn，
∴
=
，
又
=
，则
=
．
即
=
．
故答案为：
．
∴
| A5 |
| B5 |
| 5a3 |
| 5b3 |
又
| an |
| bn |
| 3n+2 |
| 4n+3 |
| a3 |
| b3 |
| 11 |
| 15 |
即
| A5 |
| B5 |
| 11 |
| 15 |
故答案为：
| 11 |
| 15 |
点评：本题考查了等差数列的性质，考查了等差数列的前n项和，是基础的计算题．
练习册系列答案
名校课堂系列答案
相关题目
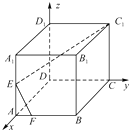在如图所示的空间直角坐标系中，正方体ABCD-A1B1C1D1棱长为2，E为正方体的棱AA1的中点，F为棱AB上的一点，且∠C1EF=90°，则点F的坐标为（ ）A、（2，
| ||
B、（2，
| ||
C、（2，
| ||
D、（2，
|
设{an}是公差不为零的等差数列，a2=2，且a1，a3，a9成等比数列，则数列{an}的前n项和Sn=（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
在△ABC中，角A，B，C对应的边分别为a，b，c．若a=1，A=30°，则“B=60°”是“b=
”的（ ）
| 3 |
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
设集合A={x|x2-x-2≤0}，B={1，2，3}，那么A∩B=（ ）
| A、{-1，0，1，2，3} |
| B、{-1，0，3} |
| C、{1，2，3} |
| D、{1，2} |
已知正方形ABCD的边长为2
命题p：?x＞0，ex＞1，则?p是（ ）
| A、?x0≤0，ex0≤1 |
| B、?x0＞0，ex0≤1 |
| C、?x＞0，ex≤1 |
| D、?x≤0，ex≤1 |
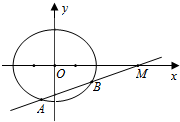如图所示，椭圆C：