题目内容
椭圆C:
+
=1(a>b>0)的两个焦点为F1(-c,0),F2(c,0),M是椭圆上的一点,且满足∠F1MF2=
.
(1)求椭圆的离心率e的取值范围;
(2)当离心率e取得最小值时,点N(0,3
)到椭圆上的点最远距离为4
,求此时椭圆C的方程;
(3)设O为坐标原点,P是椭圆C上一个动点,试求t=
的取值范围.
| x2 |
| a2 |
| y2 |
| b2 |
| π |
| 3 |
(1)求椭圆的离心率e的取值范围;
(2)当离心率e取得最小值时,点N(0,3
| 3 |
| 3 |
(3)设O为坐标原点,P是椭圆C上一个动点,试求t=
| |PF1-PF2| |
| |OP| |
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)由椭圆定义,
=
,设∠MF1F2=α,则0<α<
,由正弦定理,
=
=
,由此能求出离心率e的取值范围是[
,1).
(2)e=
时,a=2c,b=
c,设P(2ccost,
csint),则PN2=(2ccost)2+(
csint-3
)2=-(csint+9)2+4c2+108,由|PN|≤4
,得c2+6c-7=0,c>0,由此能求出椭圆的方程.
(3)当P由上顶点向右顶点运动时,|t|由0增大至
=1-e,由此能求出t的取值范围.
| c |
| a |
| |F1F2| |
| |MF1|+|MF2| |
| 2π |
| 3 |
| c |
| a |
sin
| ||
sinα+sin(
|
| 1 | ||
2cos(
|
| 1 |
| 2 |
(2)e=
| 1 |
| 2 |
| 3 |
| 3 |
| 3 |
| 3 |
| 3 |
(3)当P由上顶点向右顶点运动时,|t|由0增大至
| a-c |
| a |
解答:
解:(1)由椭圆定义,
=
,
设∠MF1F2=α,∵∠F1MF2=
,∴0<α<
,
由正弦定理,
=
=
=
,
∵cos(
-α)的值域是(
,1],
∴离心率e=
的取值范围是[
,1).
(2)e=
时,a=2c,b=
c,设P(2ccost,
csint),
则PN2=(2ccost)2+(
csint-3
)2
=4c2[1-(sint)2]+3c2(sint)2-18csint+27
=-c2(sint)2-18csint+4c2+27
=-(csint+9)2+4c2+108,
∵|PN|≤4
,∴sint=-1时PN2取最大值3c2+18c+27=48,
∴c2+6c-7=0,c>0,
∴c=1,a=2,b=
,椭圆的方程是
+y2=1.
(3)当P由上顶点向右顶点运动时,|t|由0增大至
=1-e,
∵离心率e=
的取值范围是[
,1).
∴t的取值范围是(-
,
).
| c |
| a |
| |F1F2| |
| |MF1|+|MF2| |
设∠MF1F2=α,∵∠F1MF2=
| π |
| 3 |
| 2π |
| 3 |
由正弦定理,
| c |
| a |
sin
| ||
sinα+sin(
|
=
sin
| ||||
2sin
|
=
| 1 | ||
2cos(
|
∵cos(
| π |
| 3 |
| 1 |
| 2 |
∴离心率e=
| c |
| a |
| 1 |
| 2 |
(2)e=
| 1 |
| 2 |
| 3 |
| 3 |
则PN2=(2ccost)2+(
| 3 |
| 3 |
=4c2[1-(sint)2]+3c2(sint)2-18csint+27
=-c2(sint)2-18csint+4c2+27
=-(csint+9)2+4c2+108,
∵|PN|≤4
| 3 |
∴c2+6c-7=0,c>0,
∴c=1,a=2,b=
| 3 |
| x2 |
| 4 |
(3)当P由上顶点向右顶点运动时,|t|由0增大至
| a-c |
| a |
∵离心率e=
| c |
| a |
| 1 |
| 2 |
∴t的取值范围是(-
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查椭圆的离心率的取值范围的求法,考查椭圆方程的求法,考查实数的取值范围的求不法,解题时要认真审题,注意正弦定理的合理运用.

练习册系列答案
相关题目
下列函数中,最小正周期为π的是( )
A、y=tan
| ||
| B、y=cos2x | ||
C、y=sin(x-
| ||
| D、y=sin4x |
设函数f(x)满足xf′(x)+f(x)=
,f(e)=
,则函数f(x)( )
| lnx |
| x |
| 1 |
| e |
| A、在(0,e)上单调递增,在(e,+∞)上单调递减 |
| B、在(0,+∞)上单调递增 |
| C、在(0,e)上单调递减,在(e,+∞)上单调递增 |
| D、在(0,+∞)上单调递减 |
设随机变量ξ~N(1,σ2),若P(0<ξ<1)=0.3,则P(ξ<2)=( )
| A、0.2 | B、0.7 |
| C、0.8 | D、0.5 |
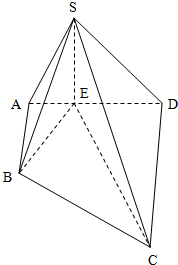 如图,在四棱锥S-ABCD中,AB∥CD,∠BAD=90°,平面SAD⊥平面ABCD,SE⊥AD于点E,CD=DE=2AB=2AE,
如图,在四棱锥S-ABCD中,AB∥CD,∠BAD=90°,平面SAD⊥平面ABCD,SE⊥AD于点E,CD=DE=2AB=2AE,