题目内容
18.设函数f(x)是奇函数,且满足f(x+2)=f(x),当0≤x≤1时,f(x)=2x(1-x),则f(-$\frac{9}{2}$)=-$\frac{1}{2}$.分析 根据题意,有函数的奇偶性可得f(-$\frac{9}{2}$)=-f($\frac{9}{2}$),结合f(x+2)=f(x),分析可得函数f(x)的周期T=2,进而可得f($\frac{9}{2}$)=f($\frac{9}{2}$-2×2)=f($\frac{1}{2}$),结合函数的解析式可得f($\frac{1}{2}$)的值,又由于f(-$\frac{9}{2}$)=-f($\frac{9}{2}$),即可得答案.
解答 解:根据题意,函数f(x)为奇函数,则有f(-$\frac{9}{2}$)=-f($\frac{9}{2}$),
又由函数f(x)满足f(x+2)=f(x),
函数f(x)的周期T=2,
则f($\frac{9}{2}$)=f($\frac{9}{2}$-2×2)=f($\frac{1}{2}$),
又由当0≤x≤1时,f(x)=2x(1-x),
则f($\frac{1}{2}$)=2×$\frac{1}{2}$×(1-$\frac{1}{2}$)=$\frac{1}{2}$,
故f(-$\frac{9}{2}$)=-f($\frac{9}{2}$)=-$\frac{1}{2}$;
故答案为:-$\frac{1}{2}$.
点评 本题考查函数的奇偶性与周期性,关键是利用函数的奇偶性与周期性,分析得到f(-$\frac{9}{2}$)与f($\frac{1}{2}$)的关系.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目
13.函数f(x)=$\left\{\begin{array}{l}{lo{g}_{2}x,x>0}\\{{3}^{x},x≤0}\end{array}\right.$,则f(f($\frac{1}{4}$))=( )
| A. | $\frac{1}{9}$ | B. | $\frac{1}{6}$ | C. | $\frac{1}{3}$ | D. | 1 |
3.已知α,β∈(0,π),且tan(α-β)=$\frac{1}{2}$,tanβ=-$\frac{1}{7}$,则2α-β的值是( )
| A. | -$\frac{π}{4}$ | B. | -$\frac{3π}{4}$ | C. | $\frac{π}{4}$ | D. | $\frac{3π}{4}$ |
10.某班对一次实验成绩进行分析,利用随机数表法抽取样本时,先将50个同学按01,02,03…50进行编号,然后从随机数表第9行第11列的数开始向右读,则选出的第7个个体是( )
(注:表为随机数表的第8行和第9行)

(注:表为随机数表的第8行和第9行)

| A. | 02 | B. | 13 | C. | 42 | D. | 44 |
7.若集合A={x|3x-x2>0},集合B={x|x<1},则A∩(∁UB)等于( )
| A. | (-3,1] | B. | (-∞,1] | C. | [1,3) | D. | (3,+∞) |
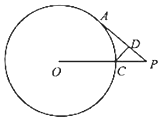 如图,过圆O外一点P作圆O的切线PA,切点为A,连接OP与圆O交于点C,过点C作圆O作AP的垂线,垂足为D,若PA=2$\sqrt{5}$,PC:PO=1:3,求CD的长.
如图,过圆O外一点P作圆O的切线PA,切点为A,连接OP与圆O交于点C,过点C作圆O作AP的垂线,垂足为D,若PA=2$\sqrt{5}$,PC:PO=1:3,求CD的长.