题目内容
11．已知函数f（x）=-x3+ax2+b（a，b∈R）．（1）设函数g（x）=f（x）-b，若a=1，求函数g（x）在（1，g（1））处的切线方程；
（2）若函数f（x）在（0，2）上是增函数，求a的取值范围．
分析 （1）求得g（x）的解析式和导数，可得切线的斜率和切点，由点斜式方程，可得切线的方程；
（2）先求出f（x）的导函数，然后求出导函数的根，讨论a的取值范围分别求出函数的单调增区间，使（0，2）是增区间的子集即可，解不等式即可得到所求a的范围．
解答 解：（1）函数g（x）=f（x）-b=-x3+x2，
导数为g′（x）=-3x2+2x，
函数g（x）在（1，g（1））处的切线斜率为-3+2=-1，
切点为（1，0），可得切线的方程为y=-（x-1），
即x+y-1=0；
（2）由题意，得f'（x）=-3x2+2ax，
令f′（x）=0，解得x=0或x=$\frac{2}{3}$a，
当a＜0时，由f′（x）＞0，解得$\frac{2a}{3}$＜x＜0，
所以f（x）在（$\frac{2a}{3}$，0）上是增函数，与题意不符，舍去；
当a=0时，由f'（x）=-3x2≤0，与题意不符，舍去；
当a＞0时，由f′（x）＞0，解得0＜x＜$\frac{2a}{3}$，
所以f（x）在（0，$\frac{2a}{3}$）上是增函数，
又f（x）在（0，2）上是增函数，
所以$\frac{2a}{3}$≥2，解得a≥3，
综上，a的取值范围为[3，+∞）．
点评 本题主要考查了利用导数研究函数的单调性，以及转化思想和分类讨论的综合运用，属于中档题．
练习册系列答案
相关题目
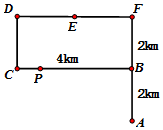8月27日我校组织了高一学生拉练活动，步行路线如图：A→B→C→D→E→F→A（A是学校，BCDF为矩形，AB=BF=2km，BC=4km），步行匀速前进，速度4km/h，拉练过程中在DF的中点E处休息了半小时，从学校A点出发开始计时，经过t小时到达P点，P到A的直线距离为|PA|，设y=|PA|2．
10．已知f（x）=sin2x+$\sqrt{3}$cos2x（x∈R），函数y=f（x+φ）的图象关于直线x=0对称，则φ的值可以是（ ）
| A． | $\frac{π}{6}$ | B． | $\frac{π}{3}$ | C． | $\frac{π}{4}$ | D． | $\frac{π}{12}$ |