题目内容
17.下列导数运算正确的是( )| A. | (x+$\frac{1}{x}$)′=1+$\frac{1}{{x}^{2}}$ | B. | (xlnx)′=lnx+1 | C. | (cosx)′=sinx | D. | (2x)′=x2x-1 |
分析 根据函数的导数的公式分别进行判断即可.
解答 解:A.(x+$\frac{1}{x}$)′=1-$\frac{1}{{x}^{2}}$,故A错误,
B.(xlnx)′=lnx+x•$\frac{1}{x}$=lnx+1,故B正确,
C.(cosx)′=-sinx,故C错误,
D.(2x)′=2xln2,故D正确,
故选:B
点评 本题主要考查导数的计算,根据函数的导数公式是解决本题的关键.

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案
相关题目
5.一台机器由于使用时间较长,但还可以使用,它按不同的转速生产出来的某机器零件有一些会有缺点,每小时生产有缺点零件的多少随机器运转的速度而变化,如表是抽样试验结果:
若实际生产中,允许每小时的产品中有缺点的零件数最多为10个,那么机器的转速应该控制所在的范围是( )
| 转速x/(rad/s) | 16 | 14 | 12 | 8 |
| 每小时生产有缺点的零件数y/件 | 11 | 9 | 8 | 5 |
| A. | 10转/s以下 | B. | 15转/s以下 | C. | 20转/s以下 | D. | 25转/s以下 |
2.已知命题p:“x∈R时,都有x2-x+$\frac{1}{4}$<0”;命题q:“存在x∈R,使sinx+cosx=$\sqrt{2}$成立”.则下列判断正确的是( )
| A. | p∨q为假命题 | B. | p∧q为真命题 | C. | ¬p∧q为真命题 | D. | ¬p∨¬q是假命题 |
9.已知集合M={x|-2≤x≤2},N={x|y=$\sqrt{1-x}$},那么M∩N=( )
| A. | [-2,1] | B. | (-2,1) | C. | (-2,1] | D. | {-2,1} |
7.设A={x∈Z|x≤6},B={x∈Z|x>1},那么A∩B等于( )
| A. | {x|1<x≤6} | B. | {1,2,3,4,5,6} | C. | {2,3,4,5,6} | D. | {2,3,4,5} |
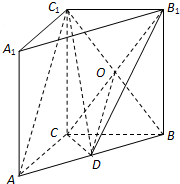 (理科做)如图,在直三棱柱ABC-A1B1C1中,AC⊥BC,点D是AB的中点.
(理科做)如图,在直三棱柱ABC-A1B1C1中,AC⊥BC,点D是AB的中点.