题目内容
3.设等差数列{an}的前n项和为Sn,若a5=3,S10=40,则nSn的最小值为-32.分析 利用等差数列的通项公式与求和公式可得Sn,再利用数列的单调性即可得出.
解答 解:设等差数列{an}的公差为d,∵a5=3,S10=40,
∴a1+4d=3,10a1+$\frac{10×9}{2}$d=40,
解得a1=-5,d=2.
∴Sn=-5n+$\frac{n(n-1)}{2}×2$=n2-6n.
则nSn=n2(n-6).
n≤5时,nSn<0.
n≥6时,nSn≥0.
可得:n=4时,nSn取得最小值-32.
故答案为:-32.
点评 本题考查了等差数列的通项公式与求和公式、数列的单调性,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
14.已知函数f(x)满足xf′(x)-f(x)=xex且f(-1)=$\frac{1}{e}$,则x<0时f(x)=( )
| A. | 既有极大值又有极小值 | B. | 有极大值无极小值 | ||
| C. | 既无极大值又无极小值 | D. | 有极小值无极大值 |
11.在一次实验中,测得(x,y)的四组值分别是A(6,2),B(8,3),C(10,5),D(12,6),则y与x之间的回归直线方程为( )
| A. | $\hat y=2.3x-0.7$ | B. | $\hat y=2.3x+0.7$ | C. | $\hat y=0.7x-2.3$ | D. | $\hat y=0.7x+2.3$ |
15.曲线y=3lnx+x+2在点p0处的切线与直线x+4y-8=0垂直,则点p0的坐标是( )
| A. | (0,1) | B. | (1,0) | C. | (1,-1) | D. | (1,3) |
12.某三棱锥的三视图如图所示,已知该三棱锥的外接球的表面积为12π,则此三棱锥的体积为( )
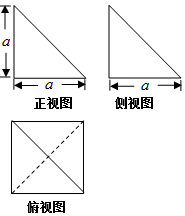

| A. | 4 | B. | $\frac{4}{3}$ | C. | $\frac{8}{3}$ | D. | $\frac{1}{3}$ |