题目内容
已知圆心为C的圆,满足下列条件:圆心C位于x轴正半轴上,与直线3x-4y+7=0相切,且被 轴截得的弦长为
轴截得的弦长为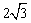 ,圆C的面积小于13.
,圆C的面积小于13.
(Ⅰ)求圆C的标准方程;
(Ⅱ)设过点M(0,3)的直线l与圆C交于不同的两点A,B,以OA,OB为邻边作平行四边形OADB.是否存在这样的直线l,使得直线OD与MC恰好平行?如果存在,求出l的方程;如果不存在,请说明理由.
解:(I)设圆C:(x-a)2+y2=R2(a>0),由题意知
 解得a=1 或 a=
解得a=1 或 a= ,
,
又∵ S=πR2<13,
∴ a=1,
∴ 圆C的标准方程为:(x-1)2+y2=4.
(Ⅱ)当斜率不存在时,直线l为:x=0不满足题意.
当斜率存在时,设直线l:y=kx+3,A(x1,y1),B(x2,y2),
又∵ l与圆C相交于不同的两点,
联立 消去y得:(1+k2)x2+(6k-2)x+6=0,
消去y得:(1+k2)x2+(6k-2)x+6=0,
∴Δ=(6k-2)2-24(1+k2)=36k2-6k-5>0,
解得 或
或 .
.
x1+x2= ,y1+ y2=k(x1+x2)+6=
,y1+ y2=k(x1+x2)+6= ,
,
 ,
, ,
,
假设 ∥
∥ ,则
,则 ,
,
∴  ,
,
解得 ,假设不成立.
,假设不成立.
∴ 不存在这样的直线l.

练习册系列答案
相关题目
 ,
, ,则下列说法正确的是 ( )
,则下列说法正确的是 ( ) 与
与 一定相交 (B)
一定相交 (B)  ,若点
,若点 为平面区域
为平面区域 上的一个动点,则|AM|的最小值是
上的一个动点,则|AM|的最小值是 B.
B. C.
C. D.
D.
 上的任意一点,若∠PF1F2=α,∠PF2F1=β,且cosα=
上的任意一点,若∠PF1F2=α,∠PF2F1=β,且cosα= ,sin(α+β)=
,sin(α+β)= ,则此椭圆的离心率为 .
,则此椭圆的离心率为 . ”是“
”是“ ”的
”的 ,
, ,
, ,则
,则 ________.
________. 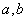 及平面
及平面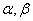 ,下列命题中正确的是
,下列命题中正确的是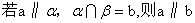 B.
B. 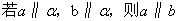
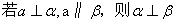 D.
D. 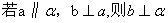
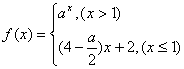 是实数集上的单调递增函数,则实数
是实数集上的单调递增函数,则实数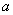 的取值范围是( )
的取值范围是( )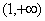 B.
B.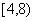 C.
C.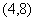 D.
D.