Question

正方体ABCD-A₁B₁C₁D₁中，直线A₁B和平面A₁B₁CD所成的角为（　　）

• A、30°
• B、45°
• C、60°
• D、15°

Answer 1

考点：直线与平面所成的角

专题：空间角

分析：以D为原点，建立空间直角坐标系，利用向量法能求出直线A₁B和平面A₁B₁CD所成的角．

解答： 解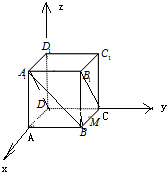：以D为原点，建立空间直角坐标系，
设正方体ABCD-A₁B₁C₁D₁的棱长为1，
则A₁（1，0，1），B（1，1，0），D（0，0，0），C（0，1，0），

A1B

=（0，1，-1），

DA1

=（1，0，1），

DC

=（0，1，0），
设平面A₁B₁CD的法向量

n

=(x，y，z)，
则

n • DA1 =x+z=0 n • DC =y=0

，
取x=1，得

n

=（1，0，-1），
设直线A₁B和平面A₁B₁CD所成的角为θ，
sinθ=|cos＜

A1B

，

n

＞|=|

1

2 × 2

|=

1

2

，
∴直线A₁B和平面A₁B₁CD所成的角为30°．
故选：A．

点评：本题考查直线与平面所成的角的求法，是基础题，解题时要认真审题，注意向量法的合理运用．