题目内容
18．已知p：x2+2x-3＜0；q：1-a≤x≤1+a，且q是p的必要不充分条件，则a的取值范围是（ ）| A． | （4，+∞） | B． | （-∞，0] | C． | [4，+∞） | D． | （-∞，0） |
分析 p：x2+2x-3＜0，解得-3＜x＜1．由于q是p的必要不充分条件，可得$\left\{\begin{array}{l}{1-a≤-3}\\{1＜1+a}\end{array}\right.$，解得a范围即可．
解答 解：p：x2+2x-3＜0，解得-3＜x＜1；
q：1-a≤x≤1+a，
∵q是p的必要不充分条件，
∴$\left\{\begin{array}{l}1-a≤-3\\ 1≤1+a\end{array}\right.$，解得a≥4．
故选：C．
点评 本题考查了简易逻辑的判定方法、不等式的性质，考查了推理能力与计算能力，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
9．函数y=2sin（ωx+φ）的部分图象如图所示，则ω，φ可以取的一组值是（ ）
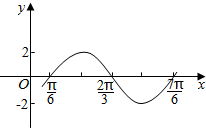
| A． | ω=2，φ=-$\frac{π}{3}$ | B． | ω=2，φ=$\frac{π}{3}$ | C． | ω=2，ω=-$\frac{π}{6}$ | D． | ω=1，φ=$\frac{π}{6}$ |
6．已知实数x、y满足$\left\{\begin{array}{l}{x-y-1≤0}\\{2x-y-3≥0}\end{array}\right.$，在区间（0，5）内任取两数a、b．则目标函数z=ax+by的最小值大于2$\sqrt{5}$的概率为（ ）
| A． | $\frac{1}{5}$ | B． | $\frac{2}{5}$ | C． | $\frac{3}{5}$ | D． | $\frac{4}{5}$ |
13．已知两条直线：y=（a-1）x-2和3x+（a+3）y-1=0互相平行，则a等于 （ ）
| A． | 0 或-2 | B． | -2 或-1 | C． | 1或-2 | D． | 0或2 |
3．函数y=x${\;}^{\frac{1}{2}}$的定义域为（ ）
| A． | {x|x≠0} | B． | {x|x≥0} | C． | {x|x＞0} | D． | R |
10．下列四组函数中，表示相等函数的一组是（ ）
| A． | f（x）=1，f（x）=x0 | B． | f（x）=|x|，f（t）=$\sqrt{t^2}$ | ||
| C． | f（x）=$\frac{x^2-1}{x-1}$，g（x）=x+1 | D． | f（x）=$\sqrt{x+1}$•$\sqrt{x-1}$，g（x）=$\sqrt{x^2-1}$ |
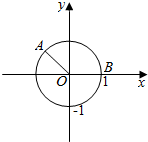已知点A，B在单位圆上，A（-$\frac{3}{5}$，$\frac{4}{5}$），B（1，0），∠BOA=a，如图所示