题目内容
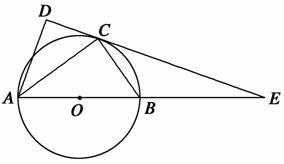
如图,△ABO三边上的点C、D、E都在⊙O上,已知AB∥DE,AC=CB.
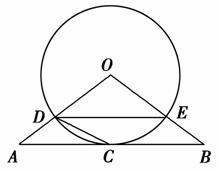
(1)求证:直线AB是⊙O的切线;
(2)若AD=2,且tan∠ACD=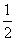 ,求⊙O的半径r的长.
,求⊙O的半径r的长.
(1)∵AB∥DE,∴ =
= ,
,
又OD=OE,∴OA=OB.
如图,连接OC,∵AC=CB,∴OC⊥AB.
又点C在⊙O上,∴直线AB是⊙O的切线.

(2)如图,延长DO交⊙O于点F,连接FC.
由(1)知AB是⊙O的切线,
∴弦切角∠ACD=∠F,
∴△ACD∽△AFC.
∴tan∠ACD=tan∠F=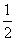 ,又∠DCF=90°,∴
,又∠DCF=90°,∴ =
=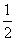 .
.
∴ =
= =
=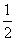 ,而AD=2,得AC=4.
,而AD=2,得AC=4.
又AC2=AD·AF,
∴2·(2+2r)=42,于是r=3.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
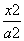 +
+ =1(a>b>0)的不平行于对称轴且不过原点的弦,M为AB的中点,则kOM·kAB=-
=1(a>b>0)的不平行于对称轴且不过原点的弦,M为AB的中点,则kOM·kAB=-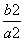 .那么对于双曲线则有如下命题:AB是双曲线
.那么对于双曲线则有如下命题:AB是双曲线
 的⊙O中,弦AB、CD相交于点P,PA=PB=2,PD=1,则圆心O到弦CD的距离为________.
的⊙O中,弦AB、CD相交于点P,PA=PB=2,PD=1,则圆心O到弦CD的距离为________.
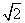 ,求BC的长.
,求BC的长.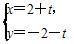 (t为参数)与圆C:
(t为参数)与圆C: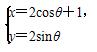 (θ为参数),则直线l的倾斜角及圆心C的直角坐标分别为( )
(θ为参数),则直线l的倾斜角及圆心C的直角坐标分别为( ) ,(1,0) B
,(1,0) B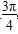 ,(1,0) D.
,(1,0) D. (t为参数),若以直角坐标系的原点为极点,x轴的正半轴为极轴建立极坐标系,则曲线C的极坐标方程为________.
(t为参数),若以直角坐标系的原点为极点,x轴的正半轴为极轴建立极坐标系,则曲线C的极坐标方程为________.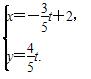 (t为参数).
(t为参数).