题目内容
已知f(n)＝1＋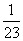
＋
＋
＋…＋
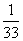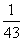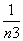，g(n)＝
－
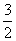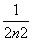，n∈N*.
(1)当n＝1,2,3时，试比较f(n)与g(n)的大小；
(2)猜想f(n)与g(n)的大小关系，并给出证明．
(1)当n＝1时，f(1)＝1，g(1)＝1，
所以f(1)＝g(1)；
当n＝2时，f(2)＝
，g(2)＝
，
所以f(2)<g(2)；
当n＝3时，f(3)＝
，g(3)＝
，
所以f(3)<g(3)．
(2)由(1)猜想f(n)≤g(n)，下面用数学归纳法给出证明．
①当n＝1,2,3时，不等式显然成立．
②假设当n＝k(k≥3，k∈N*)时不等式成立，
即1＋＋＋＋…＋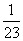
<－
，
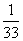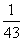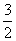那么，当n＝k＋1时，
，
所以f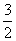(k＋1)<－
＝g(k＋1)．
由①②可知，对一切n∈N*，
都有f(n)≤g(n)成立．
练习册系列答案
相关题目
＝1＋bi，其中a，b是实数，i是虚数单位，则a＋bi＝( )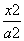
＋
＝1(a>b>0)的不平行于对称轴且不过原点的弦，M为AB的中点，则kOM·kAB＝－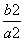
.那么对于双曲线则有如下命题：AB是双曲线
，
，
，
，
，
，
，
，
，
，…，
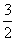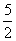…，则a2012＝________.
(n∈N*)的第二步中，当n＝k＋1时等式左边与n＝k时等式左边的差等于________．
＋n，an>0(n∈N*)．
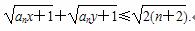
的⊙O中，弦AB、CD相交于点P，PA＝PB＝2，PD＝1，则圆心O到弦CD的距离为________．
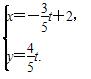(t为参数)．