题目内容
已知函数f(x)=cos(2x-
)+sin2x-cos2x.
(1)求f(x)的单调递增区间;
(2)用“五点法”画出函数f(x)在一个周期内的简图.
| π |
| 3 |
(1)求f(x)的单调递增区间;
(2)用“五点法”画出函数f(x)在一个周期内的简图.
考点:五点法作函数y=Asin(ωx+φ)的图象,三角函数中的恒等变换应用
专题:作图题,三角函数的图像与性质
分析:(1)利用三角函数的恒等变换,化简f(x),求出函数的单调递增区间;
(2)列出关于x、y变化的表格,根据表中数据,画出函数在一个周期的图象.
(2)列出关于x、y变化的表格,根据表中数据,画出函数在一个周期的图象.
解答:
解:(1)∵f(x)=
cos2x+
sin2x-cos2x
=
sin2x-
cos2x
=sin(2x-
),
令2kπ≤2x-
≤
+2kπ,k∈Z,
则kπ-
≤x≤
+kπ,k∈Z;
∴函数f(x)的单调递增区间是[kπ-
,
+kπ],k∈Z;
(2)列表如下;
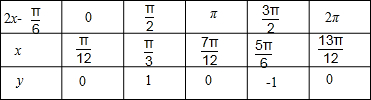
根据表中数据,建立平面直角坐标系,画出函数在一个周期的图象如下;
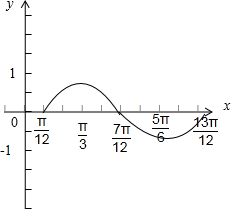 .
.
| 1 |
| 2 |
| ||
| 2 |
=
| ||
| 2 |
| 1 |
| 2 |
=sin(2x-
| π |
| 6 |
令2kπ≤2x-
| π |
| 6 |
| π |
| 2 |
则kπ-
| π |
| 6 |
| π |
| 3 |
∴函数f(x)的单调递增区间是[kπ-
| π |
| 6 |
| π |
| 3 |
(2)列表如下;

根据表中数据,建立平面直角坐标系,画出函数在一个周期的图象如下;
 .
.
点评:本题考查了三角函数的恒等变换以及三角函数的图象与性质的应用问题,也考查了作图能力,是基础题.

练习册系列答案
 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
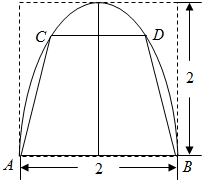 如图,有一块抛物线形状的钢板,计划将此钢板切割成等腰梯形ABCD的形状,使得A,B,C,D都落在抛物线上,点A,B关于抛物线的轴对称,且AB=2,抛物线的顶点到底边的距离是2,记CD=2t,梯形面积为S.
如图,有一块抛物线形状的钢板,计划将此钢板切割成等腰梯形ABCD的形状,使得A,B,C,D都落在抛物线上,点A,B关于抛物线的轴对称,且AB=2,抛物线的顶点到底边的距离是2,记CD=2t,梯形面积为S. 如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=
如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=