题目内容
已知F1，F2是双曲线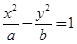
（a>0，b>0）的左，右焦点，过F1且垂直于x轴的直线与双曲线交于A，B两点，若△
为正三角形，则该双曲线的离心率为（ ）
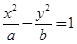（a>0，b>0）的左，右焦点，过F1且垂直于x轴的直线与双曲线交于A，B两点，若△为正三角形，则该双曲线的离心率为（ ）| A．2 | B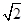． | C．3 | D． |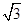
D
解：设F1（-c，0），F2（c，0），则
将F1（-c，0）代入双曲线C：
，可得
，
∴y=±
∵过F1且垂直于x轴的直线与双曲线C交于A、B两点，
∴|AB|=2
∵△ABF2为等边三角形，|F1F2|=2c，
∴2c=
×2
∴2ac=" 3" (c2-a2)
∴ 3 e2-2e-1=0
∴e="-"
或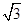
∵e＞1，∴e=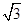
故选D．
将F1（-c，0）代入双曲线C：
，可得，∴y=±
∵过F1且垂直于x轴的直线与双曲线C交于A、B两点，∴|AB|=2
∵△ABF2为等边三角形，|F1F2|=2c，
∴2c=
×2∴2ac=" 3" (c2-a2)
∴ 3 e2-2e-1=0
∴e="-"
或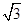∵e＞1，∴e=
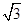
故选D．
练习册系列答案
阅读快车系列答案
相关题目
有共同渐近线，并且经过点 （－3，
）的双曲线方程.
的左．右焦点分别为
,线段
被抛物线
的焦点分成7：5的两段，则此双曲线的离心率为
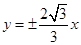，双曲线过点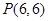
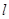经过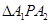
的重心G，与双曲线交于不同的两点M、N，问:是否存在直线
的双曲线的标准方程为 。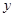
轴上的双曲线渐近线方程为
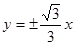,且离心率为2，已知点A（
）
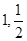的右支上存在一点，它到右焦点及左准线的距离相等，则双曲线离心率的取值范围是 ( )
，
，
是此双曲线上一点，若
，
，则该双曲线的方程是_____________。
过双曲线
的右焦点且与双曲线的两条渐近线分别交于
，
两点，若原点在以
为直径的圆外，则双曲线离心率的取值范围是 ( )
