题目内容
(12)设焦点在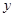 轴上的双曲线渐近线方程为
轴上的双曲线渐近线方程为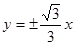 ,且离心率为2,已知点A(
,且离心率为2,已知点A(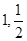 )
)
(1)求双曲线的标准方程;
(2)过点A的直线L交双曲线于M,N两点,点A为线段MN的中点,求直线L方程。
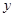 轴上的双曲线渐近线方程为
轴上的双曲线渐近线方程为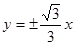 ,且离心率为2,已知点A(
,且离心率为2,已知点A(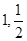 )
)(1)求双曲线的标准方程;
(2)过点A的直线L交双曲线于M,N两点,点A为线段MN的中点,求直线L方程。
解:(1)
 ;(2)
;(2)
本试题主要是考查了双曲线的方程的求解,以及直线与双曲线的位置关系的运用。
中点弦问题的重点运用。
(1)利用已知函数的离心率和渐近线方程可知双曲线的标准方程。
(2)设出直线方程与双曲线联立,借助于韦达定理和两点的斜率公式可知得到斜率的值,进而求解得到直线的方程。
解:(1)
(2)设直线l:

中点弦问题的重点运用。
(1)利用已知函数的离心率和渐近线方程可知双曲线的标准方程。
(2)设出直线方程与双曲线联立,借助于韦达定理和两点的斜率公式可知得到斜率的值,进而求解得到直线的方程。
解:(1)

(2)设直线l:


练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
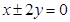 ,焦距为
,焦距为 ,这双曲线的方程为_______________
,这双曲线的方程为_______________ 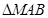 是直角三角形,则此双曲线的离心率e的值为 ( )
是直角三角形,则此双曲线的离心率e的值为 ( )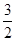
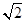
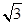
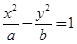 (a>0,b>0)的左,右焦点,过F1且垂直于x轴的直线与双曲线交于A,B两点,若△
(a>0,b>0)的左,右焦点,过F1且垂直于x轴的直线与双曲线交于A,B两点,若△ 为正三角形,则该双曲线的离心率为( )
为正三角形,则该双曲线的离心率为( )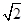
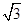
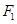 、
、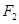 为双曲线
为双曲线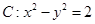 的左、右焦点,点
的左、右焦点,点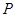 在
在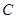 上,
上,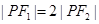 ,则
,则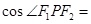
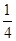
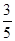
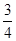
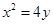 的焦点为
的焦点为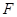 ,过焦点
,过焦点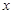 轴的动直线
轴的动直线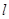 交抛物线于
交抛物线于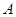 ,
,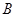 两点,抛物线在
两点,抛物线在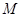 .
.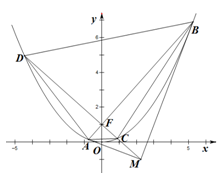

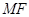 交该抛物线于
交该抛物线于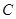 ,
,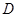 两点,求四边形
两点,求四边形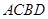 面积的最小值.
面积的最小值. 的渐近线夹角为
的渐近线夹角为 ,则cos
,则cos 的值为_____________
的值为_____________ 的渐近线方程是( )
的渐近线方程是( )



 的焦点到渐近线的距离为( )
的焦点到渐近线的距离为( )
