题目内容
(本大题满分14分)
已知中心在原点,顶点A1、A2在x轴上,其渐近线方程是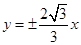 ,双曲线过点
,双曲线过点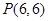
(1)求双曲线方程
(2)动直线 经过
经过 的重心G,与双曲线交于不同的两点M、N,问:是否存在直线
的重心G,与双曲线交于不同的两点M、N,问:是否存在直线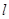 ,使G平分线段MN,证明你的结论
,使G平分线段MN,证明你的结论
已知中心在原点,顶点A1、A2在x轴上,其渐近线方程是
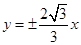 ,双曲线过点
,双曲线过点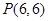
(1)求双曲线方程
(2)动直线
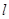 经过
经过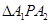 的重心G,与双曲线交于不同的两点M、N,问:是否存在直线
的重心G,与双曲线交于不同的两点M、N,问:是否存在直线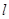 ,使G平分线段MN,证明你的结论
,使G平分线段MN,证明你的结论(1)所求双曲线方程为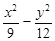 ="1" ;
="1" ;
(2)所求直线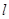 不存在。
不存在。
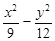 ="1" ;
="1" ;(2)所求直线
 不存在。
不存在。本试题主要是考查了双曲线方程的求解,已知直线与双曲线的位置关系的综合运用。
(1)利用已知中的渐近线方程是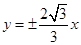 ,双曲线过点
,双曲线过点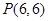
那么设出双曲线的标准方程,然后代入点和a,b的关系得到求解。
(2)假设存在直线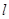 ,使G(2,2)平分线段MN,那么利用对称性,分别设出点的坐标,那么联立方程组,可知斜率,得到直线的方程,从而验证是否存在。
,使G(2,2)平分线段MN,那么利用对称性,分别设出点的坐标,那么联立方程组,可知斜率,得到直线的方程,从而验证是否存在。
(1)如图,设双曲线方程为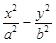 =1 …………1分
=1 …………1分
由已知得 ………………………………………3分
………………………………………3分
解得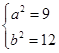 …………………………………………………5分
…………………………………………………5分
所以所求双曲线方程为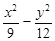 ="1" ……………………6分
="1" ……………………6分
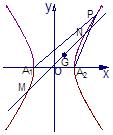
(2)P、A1、A2的坐标依次为(6,6)、(3,0)、(-3,0),
∴其重心G的坐标为(2,2)…………………………………………………………8分
假设存在直线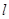 ,使G(2,2)平分线段MN,
,使G(2,2)平分线段MN,
设M(x1,y1),N(x2,y2) 则有
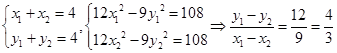 ,∴kl=
,∴kl=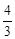 ……………………10分
……………………10分
∴l的方程为y=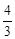 (x-2)+2,12分
(x-2)+2,12分
由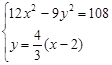 ,消去y,整理得x2-4x+28="0"
,消去y,整理得x2-4x+28="0"
∵Δ=16-4×28<0,∴所求直线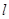 不存在…………………………………………14分
不存在…………………………………………14分
(1)利用已知中的渐近线方程是
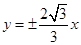 ,双曲线过点
,双曲线过点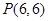
那么设出双曲线的标准方程,然后代入点和a,b的关系得到求解。
(2)假设存在直线
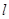 ,使G(2,2)平分线段MN,那么利用对称性,分别设出点的坐标,那么联立方程组,可知斜率,得到直线的方程,从而验证是否存在。
,使G(2,2)平分线段MN,那么利用对称性,分别设出点的坐标,那么联立方程组,可知斜率,得到直线的方程,从而验证是否存在。(1)如图,设双曲线方程为
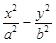 =1 …………1分
=1 …………1分
由已知得
 ………………………………………3分
………………………………………3分解得
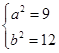 …………………………………………………5分
…………………………………………………5分 所以所求双曲线方程为
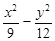 ="1" ……………………6分
="1" ……………………6分(2)P、A1、A2的坐标依次为(6,6)、(3,0)、(-3,0),
∴其重心G的坐标为(2,2)…………………………………………………………8分
假设存在直线
 ,使G(2,2)平分线段MN,
,使G(2,2)平分线段MN,设M(x1,y1),N(x2,y2) 则有
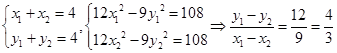 ,∴kl=
,∴kl=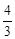 ……………………10分
……………………10分∴l的方程为y=
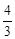 (x-2)+2,12分
(x-2)+2,12分由
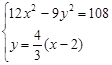 ,消去y,整理得x2-4x+28="0"
,消去y,整理得x2-4x+28="0" ∵Δ=16-4×28<0,∴所求直线
 不存在…………………………………………14分
不存在…………………………………………14分
练习册系列答案
相关题目
 的实轴长是 ( )
的实轴长是 ( ) 
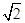
 的左、右焦点分别为
的左、右焦点分别为 为
为 的右支上一点,且
的右支上一点,且 ,则
,则 等于( )
等于( ) 是纯虚数,则圆锥曲线
是纯虚数,则圆锥曲线 的离心率为( )
的离心率为( )


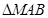 是直角三角形,则此双曲线的离心率e的值为 ( )
是直角三角形,则此双曲线的离心率e的值为 ( )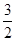
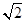
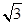
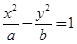 (a>0,b>0)的左,右焦点,过F1且垂直于x轴的直线与双曲线交于A,B两点,若△
(a>0,b>0)的左,右焦点,过F1且垂直于x轴的直线与双曲线交于A,B两点,若△ 为正三角形,则该双曲线的离心率为( )
为正三角形,则该双曲线的离心率为( )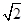
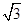
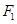 、
、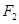 为双曲线
为双曲线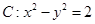 的左、右焦点,点
的左、右焦点,点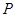 在
在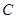 上,
上,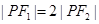 ,则
,则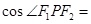
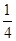
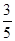
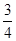
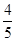
 的两条渐近线与直线
的两条渐近线与直线 围成的三角形区域(包括边界)为D,P
围成的三角形区域(包括边界)为D,P 为D内的一个动点,则目标函数
为D内的一个动点,则目标函数 的最小值为( )
的最小值为( )


 的渐近线夹角为
的渐近线夹角为 ,则cos
,则cos 的值为_____________
的值为_____________