题目内容
已知函数 .
.
⑴若 ,解方程
,解方程 ;
;
⑵若函数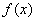 在
在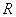 上单调递增,求实数
上单调递增,求实数 的取值范围;
的取值范围;
⑶是否存在实数 ,使不等式
,使不等式 对一切实数
对一切实数 恒成立?若存在,求出
恒成立?若存在,求出 的取值范围,若不存在,请说明理由.
的取值范围,若不存在,请说明理由.
解:(1)当 时,
时, , 故有,
, 故有,
 ,
,
当 时,由
时,由 ,有
,有 ,解得
,解得 或
或
当 时,
时, 恒成立
恒成立
∴ 方程的解集为
(2) ,
,
若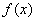 在
在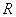 上单调递增,则有
上单调递增,则有
 , 解得,
, 解得,
∴ 当 时,
时,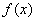 在
在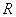 上单调递增
上单调递增
(3)设
则
不等式 对一切实数
对一切实数 恒成立,等价于不等式
恒成立,等价于不等式 对一切实数
对一切实数 恒成立.
恒成立.
①若 ,则
,则 ,即
,即 ,取
,取 ,此时
,此时
 ,
,
即对任意的 ,总能找到
,总能找到 ,使得
,使得 ,
,
∴不存在 ,使得
,使得 恒成立.
恒成立.
②若 ,
, ,
, 值域
值域 ,
,
所以 恒成立. ③若
恒成立. ③若 ,
,
当 时,
时, 单调递减,其值域为
单调递减,其值域为 ,
,
由于 ,所以
,所以 成立.
成立.
当 时,由
时,由 ,知
,知 ,
,  在
在 处取最小值,
处取最小值,
令 ,得
,得 ,又
,又 ,所以
,所以
综上, .
.

练习册系列答案
相关题目
 、b是满足
、b是满足 的实数,其中
的实数,其中 .
. ; ⑵求证:
; ⑵求证: .
. 的坐标分别是
的坐标分别是 ,
, ,
, ,
, ,动点M满足:
,动点M满足: 则
则
 中随机选取一个数
中随机选取一个数 中随机选取一个数
中随机选取一个数 ,则关于
,则关于 的方程
的方程 有两个虚根的概率是 .
有两个虚根的概率是 . 的图像关于直线
的图像关于直线 对称,则
对称,则 B.
B.
 D.
D.
 的终边经过点(
的终边经过点( ,
, ),则
),则 =( ).
=( ). (D)
(D) 

 上的奇函数f(x),满足
上的奇函数f(x),满足 ,且在区间[0,2]上是增函数,若方程
,且在区间[0,2]上是增函数,若方程 在区间[-8,8]上有四个不同的根
在区间[-8,8]上有四个不同的根 ,则
,则 =( )
=( ) .则从中任意摸出2只小球,至少得到一只白球的概率为 .
.则从中任意摸出2只小球,至少得到一只白球的概率为 .