题目内容
17.废品率x%和每吨生铁成本y(元)之间的回归直线方程为y=256+2x,表明( )| A. | 废品率每增加1%,生铁成本增加258元 | |
| B. | 废品率每增加1%,生铁成本增加2元 | |
| C. | 废品率每增加1%,生铁成本每吨增加2元 | |
| D. | 废品率不变,生铁成本为256元 |
分析 回归直线方程表示废品率x%与每吨生铁成本y(元)之间的相关关系,类比函数关系,可得回归直线方程为y=256+2x时,每增加1%,生铁成本每吨平均增加2元,分析四个答案可得结论.
解答 解:回归直线方程表示废品率x%与每吨生铁成本y(元)之间的相关关系
故回归直线方程为y=256+2x时,表明废品率每增加1%,生铁成本每吨平均增加2元.
故选:C.
点评 本题考查线性回归方程,本题解题的关键是知道当自变量增加一个单位,对应的y的值要增加.数值不是一个准确数值,而是一个平均值.

练习册系列答案
相关题目
7.已知$\vec a$=(sinx,cosx),$\vec b$=(1,$\sqrt{3}$),若$\vec a⊥\vec b$,则tanx=( )
| A. | $-\sqrt{3}$ | B. | $\sqrt{3}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $-\frac{{\sqrt{3}}}{3}$ |
12.函数y=f(x) 的图象与直线x=m的交点的个数是( )
| A. | 0 | B. | 1 | C. | 0或1 | D. | 无法确定 |
9.已知集合U={1,2,3,4},集合A={1,3,4},B={2,4},则集合(∁UA)∪B=( )
| A. | {2} | B. | {4} | C. | {1,3} | D. | {2,4} |
7.某学生记忆导数公式如下,其中错误的一个是( )
| A. | (${\frac{1}{x}}$)′=-$\frac{1}{x^2}$ | B. | (ax)=axlna | C. | (lnx)′=$\frac{1}{x}$ | D. | (sinx)′=-cosx |
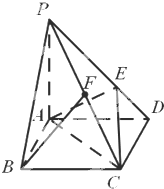 如图,在底面是菱形的四棱锥P-ABCD中,点E在PD上,且满足PE:ED=2:1,PA=AB=2,PA⊥底面ABCD,∠ABC=60°
如图,在底面是菱形的四棱锥P-ABCD中,点E在PD上,且满足PE:ED=2:1,PA=AB=2,PA⊥底面ABCD,∠ABC=60°