题目内容
14.已知函数f(x)是定义在R上的奇函数,且在区间(0,+∞)上单调,f(2)>0>f(1),则函数f(x)的零点个数为( )| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 利用函数的奇偶性以及函数的单调性,判断函数的零点个数即可.
解答 解:函数f(x)是定义在R上的奇函数,可知f(0)=0,
在区间(0,+∞)上单调,f(2)>0>f(1),
可知:x>0时,函数有一个零点,对称区间上也有一个零点,
共有3个零点.
故选:D.
点评 本题考查函数的奇偶性以及函数的单调性,函数的零点个数的判断,是基础题.

练习册系列答案
相关题目
4.已知数列{an}满足,a1=1,a2=2,an=$\frac{{{a_{n-1}}}}{{{a_{n-2}}}}$,(n≥3,n∈N*).则a2016=( )
| A. | 1 | B. | 2 | C. | $\frac{1}{2}$ | D. | 2-2016 |
9.已知集合U={1,2,3,4},集合A={1,3,4},B={2,4},则集合(∁UA)∪B=( )
| A. | {2} | B. | {4} | C. | {1,3} | D. | {2,4} |
4.函数y=x2-(4a+1)x+3a2+3a的图象与x轴交于A、B两点,若两点间的距离等于2,则a的值为( )
| A. | $\frac{3}{2}$ | B. | -$\frac{1}{2}$ | C. | $\frac{3}{2}$或-$\frac{1}{2}$ | D. | $\frac{3}{2}$或-$\frac{2}{3}$ |
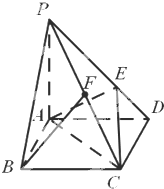 如图,在底面是菱形的四棱锥P-ABCD中,点E在PD上,且满足PE:ED=2:1,PA=AB=2,PA⊥底面ABCD,∠ABC=60°
如图,在底面是菱形的四棱锥P-ABCD中,点E在PD上,且满足PE:ED=2:1,PA=AB=2,PA⊥底面ABCD,∠ABC=60°