题目内容
在箱子里装有十张卡片，分别写有1到10的十个整数；从箱子中任取一张卡片，记下它的读数x，然后再放回箱子里；第二次再从箱子中任取一张卡片，记下它的读数y，则x+y是10的倍数的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
考点：相互独立事件的概率乘法公式
专题：概率与统计
分析：所有的读数（x，y）共有10×10=100个，其中满足x+y是10的倍数的用列举法求得共计10个，从而求得x+y是10的倍数的概率．
解答：
解：所有的读数（x，y）共有10×10=100个，其中满足x+y是10的倍数的有（1，9）、（2，8）、（3，7）、（4，6）、（5，5），
（9，1）、（8，2）、（7，3）、（6，4）、（10，10），共计10个，
故x+y是10的倍数的概率为
=
，
故选：D．
（9，1）、（8，2）、（7，3）、（6，4）、（10，10），共计10个，
故x+y是10的倍数的概率为
| 10 |
| 100 |
| 1 |
| 10 |
故选：D．
点评：本题主要考查古典概型及其概率计算公式的应用，属于基础题．
练习册系列答案
相关题目
如果程序框图的输出结果是6，那么在判断框中①表示的“条件”应该是（ ）
| A、i≥3 | B、i≥4 |
| C、i≥5 | D、i≥6 |
集合A={a，b}，B={-1，0，1}，从A到B的映射f满足f（a）+f（b）=0，那么这样的映射f的个数有（ ）
| A、2个 | B、3个 | C、5个 | D、8个 |
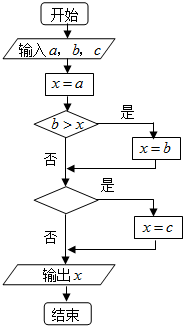如图的程序框图，如果输入三个实数a，b，c，要求输出这三个数中最大的数，那么在空白的判断框中，应该填入下面四个选项中的（ ）| A、c＞x | B、x＞a |
| C、c＞b | D、b＞c |
函数y=(1-x)
+log3x的定义域为（ ）
| 1 |
| 2 |
| A、（-∞，1] |
| B、（0，1] |
| C、（0，1） |
| D、[0，1] |