题目内容

9．已知三棱锥P-ABC的四个顶点均在同一个球面上，底面△ABC满足BA=BC=$\sqrt{6}$，$∠ABC=\frac{π}{2}$，若该三棱锥体积的最大值为3，则其外接球的体积为（　　）
A．8πB．16πC．$\frac{16}{3}$πD．$\frac{32}{3}$π

分析 求出棱锥的最大高度，利用勾股定理计算外接圆的半径，从而得出球的体积．

解答 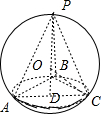解：∵△ABC是等腰直角三角形，
∴AC为截面圆的直径，故外接球的球心O在截面ABC中的射影为AC的中点D，
∴当P，O，D共线且P，O位于截面同一侧时棱锥的体积最大，棱锥的最大高度为PD，
∴$\frac{1}{3}$×$\frac{1}{2}×\sqrt{6}×\sqrt{6}$×PD=3，解得PD=3，
设外接球的半径为R，则OD=3-R，OC=R，
在△ODC中，CD=$\frac{1}{2}$AC=$\sqrt{3}$，
由勾股定理得：（3-R）2+3=R2，解得R=2．
∴外接球的体积V=$\frac{4}{3}×π×{2}^{3}$=$\frac{32π}{3}$．
故选：D．

点评 本题考查了棱锥与球的位置关系，几何体的体积计算，属于中档题．

练习册系列答案
相关题目
6．已知函数f（x）=$\sqrt{3}$sin2x+sinxcosx-$\frac{\sqrt{3}}{2}$
（1）求函数y=f（x）在[0，$\frac{π}{2}$]上的单调递增区间；
（2）将函数y=f（x）的图象向左平移$\frac{π}{6}$个单位长度，再将图象上所有点的横坐标伸长到原来的2倍（纵坐标不变），得到函数y=g（x）的图象，求证：存在无穷多个互不相同的整数x0，使得g（x0）＞$\frac{\sqrt{3}}{2}$．
20．设x，y满足约束条件$\left\{{\begin{array}{l}{2x-y-2≤0}\\{x-2y+2≥0}\\{x+y-2≥0}\end{array}}\right.$若z=mx+y取得最大值时的最优解有无穷多个，则实数m的值是（　　）
A．$-\frac{1}{2}$B．$\frac{1}{2}$C．-2D．1
17．已知f（x）=$\frac{1}{2}$x+sin（x+φ）满足g（x）=f（x）•$\frac{{2}^{x}-1}{{2}^{x}+1}$为偶函数且g（1）＜0，则函数y=f（x）的图象大致为（　　）
A．B．C．D．
4．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$（a＞b＞0）的离心率为$\frac{1}{2}$，左、右焦点分别为圆F1、F2，M是C上一点，|MF1|=2，且|$\overrightarrow{M{F}_{1}}$||$\overrightarrow{M{F}_{2}}$|=2$\overrightarrow{M{F}_{1}}•\overrightarrow{M{F}_{2}}$．
（1）求椭圆C的方程；
（2）当过点P（4，1）的动直线l与椭圆C相交于不同两点A、B时，线段AB上取点Q，且Q满足|$\overrightarrow{AP}$||$\overrightarrow{QB}$|=|$\overrightarrow{AQ}$||$\overrightarrow{PB}$|，证明点Q总在某定直线上，并求出该定直线的方程．
14．某多面体的三视图如下图所示（网格纸上小正方形的边长为1），则该多面体的表面积为（　　）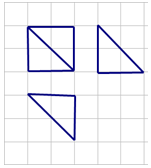
A．$8+4\sqrt{2}$B．$6+4\sqrt{2}$C．12D．$8+5\sqrt{2}$
1．已知f（x）是定义在R上的单调递增函数，则下列四个命题：①若f（x0）＞x0，则f[f（x0）]＞x0；②若f[f（x0）]＞x0，则f（x0）＞x0；③若f（x）是奇函数，则f[f（x）]也是奇函数；④若f（x）是奇函数，则f（x1）+f（x2）=0?x1+x2=0，其中正确的有（　　）
A．4个B．3个C．2个D．1个
18．曲线y=x•ex在x=1处切线的斜率等于（　　）
A．2eB．eC．2D．1
19．已知x，y满足约束条件$\left\{\begin{array}{l}{x+y-2≤0}\\{x-2y-2≤0}\\{2x-y+2≥0}\end{array}\right.$，若可行域内存在（x，y）使不等式2x+y+k≥0有解，则实数k的取值范围为[-4，+∞）．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网