题目内容
12.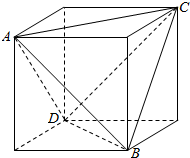 从一个正方体中,如图那样截去4个三棱锥后,得到一个正三棱锥A-BCD(底面是正三角形,各侧面是全等的等腰三角形的三棱锥叫做正三棱锥),问它的体积是正方体体积的几分之几?
从一个正方体中,如图那样截去4个三棱锥后,得到一个正三棱锥A-BCD(底面是正三角形,各侧面是全等的等腰三角形的三棱锥叫做正三棱锥),问它的体积是正方体体积的几分之几?
分析 设这个正方体的棱长为a,先求出截去的4个三棱锥的体积之和,再求出得到的正三棱锥A-BCD的体积,由此能求出结果.
解答 解:设这个正方体的棱长为a,
则如图那样截去的4个三棱锥的体积之和:V=4×($\frac{1}{3}×\frac{1}{2}{a}^{3}$)=$\frac{2}{3}{a}^{3}$,
∴得到的正三棱锥A-BCD的体积VA-BCD=${a}^{3}-\frac{2}{3}{a}^{3}$=$\frac{1}{3}{a}^{3}$,
∴它的体积是正方体体积的$\frac{1}{3}$.
点评 本题考查几何体体积的计算,是中档题,解题时要认真审题,注意正方体结构牲征的合理运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.已知数列{an}的通项公式是an=(-1)n•(3n+1),则a1+a2+…a100=( )
| A. | -300 | B. | -150 | C. | 150 | D. | 300 |
7.根据统计知识,则不正确的命题是( )
| A. | 传染病医院感染禽流感的医务人员数与医院收治的禽流感病人数是具有相关关系的两个变量 | |
| B. | 从参加高三模拟考试的1200名学生中,随机抽取100人了解试卷难易情况可以用系统抽样 | |
| C. | 回归直线$\widehat{y}$=bx+a必过样本点的中心($\overline{x}$,$\overline{y}$) | |
| D. | 对一组数据进行适当整理后,众数所在的一组频数最大 |
2.已知直线ax+2y-1=0与直线(a-4)x-ay+1=0垂直,则实数a的值为( )
| A. | 0 | B. | -4或2 | C. | 0或6 | D. | -4 |
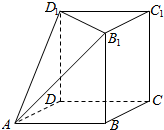 如图所示的几何体是由棱长为2cm的正方体ABCD一A1B1C1D1被平面AB1D1所截得的较大部分.
如图所示的几何体是由棱长为2cm的正方体ABCD一A1B1C1D1被平面AB1D1所截得的较大部分.