题目内容
2.已知直线ax+2y-1=0与直线(a-4)x-ay+1=0垂直,则实数a的值为( )| A. | 0 | B. | -4或2 | C. | 0或6 | D. | -4 |
分析 根据两直线垂直的性质,两直线垂直时,它们的斜率之积等于-1,解方程求得a的值.
解答 解:直线ax+2y-1=0与直线(a-4)x-ay+1=0垂直,
a≠0时,它们的斜率之积等于-1,可得-$\frac{a}{2}$×$\frac{a-4}{a}$=-1,
a=0时,直线y=$\frac{1}{2}$和x=$\frac{1}{4}$垂直,适合题意,
故选:C.
点评 本题主要考查两直线垂直的性质,两直线垂直斜率之积等于-1,属于基础题.

练习册系列答案
相关题目
13.若变量x,y满足约束条件$\left\{\begin{array}{l}{y≤x}\\{x+y≤1}\\{y≥-1}\end{array}\right.$,且z=2x+y的最大值和最小值分别为m和n,则n-m=( )
| A. | -5 | B. | -6 | C. | 5 | D. | 6 |
10.在下列函数中.值域不是[-$\sqrt{2}$,$\sqrt{2}$]的函数共有( )
①y=(sinx)′+(cosx)′②y=(sinx)′+cosx ③y=sinx+(cosx)′④y=(sinx)′•(cosx)′.
①y=(sinx)′+(cosx)′②y=(sinx)′+cosx ③y=sinx+(cosx)′④y=(sinx)′•(cosx)′.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
17.三人踢毯子,互相传递,每人每次只能踢一下,若由甲开始踢,经过4次传递后,毽子又被踢回甲,则不同的传递方式共有( )
| A. | 4种 | B. | 5种 | C. | 6种 | D. | 12种 |
12.化简$\frac{1}{\sqrt{1+ta{n}^{2}160°}}$的结果为( )
| A. | -cos160° | B. | cos160° | C. | $\frac{1}{cos160°}$ | D. | $\frac{1}{-cos160°}$ |
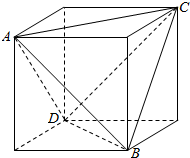 从一个正方体中,如图那样截去4个三棱锥后,得到一个正三棱锥A-BCD(底面是正三角形,各侧面是全等的等腰三角形的三棱锥叫做正三棱锥),问它的体积是正方体体积的几分之几?
从一个正方体中,如图那样截去4个三棱锥后,得到一个正三棱锥A-BCD(底面是正三角形,各侧面是全等的等腰三角形的三棱锥叫做正三棱锥),问它的体积是正方体体积的几分之几?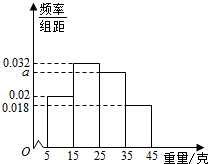 一个盒子中装有大量形状大小一样但重量不尽相同的小球,从中随机抽取50个作为样本,称出它们的重量(单位:克),重量分组区间为(5,15],(15,25](25,35],(35,45],由此得到样本的重量频率分布直方图,如图.
一个盒子中装有大量形状大小一样但重量不尽相同的小球,从中随机抽取50个作为样本,称出它们的重量(单位:克),重量分组区间为(5,15],(15,25](25,35],(35,45],由此得到样本的重量频率分布直方图,如图.