题目内容
1.若幂函数y=mxa的图象经过点($\frac{1}{4}$,$\frac{1}{2}$),则m•a的值为$\frac{1}{2}$.分析 根据幂函数的定义与性质,求出m与a的值,即可计算m•a的值.
解答 解:∵幂函数y=mxa的图象经过点($\frac{1}{4}$,$\frac{1}{2}$),
∴$\left\{\begin{array}{l}{m=1}\\{1{•(\frac{1}{4})}^{a}=\frac{1}{2}}\end{array}\right.$,
解得m=1,a=$\frac{1}{2}$;
∴m•a=1×$\frac{1}{2}$.
故答案为:$\frac{1}{2}$.
点评 本题考查了幂函数的定义与性质的应用问题,是基础题目.

练习册系列答案
相关题目
16.已知p是“?x>0,使f(x)=x+$\frac{|a-3|}{x}$的值小于2”的否定.q是“g(x)=ax2-2x在[$\frac{1}{4}$,$\frac{1}{2}$]上单调”,则p是q的( )
| A. | 充分不必要 | B. | 必要不充分 | ||
| C. | 充要 | D. | 既不充分也不必要 |
13.若变量x,y满足约束条件$\left\{\begin{array}{l}{y≤x}\\{x+y≤1}\\{y≥-1}\end{array}\right.$,且z=2x+y的最大值和最小值分别为m和n,则n-m=( )
| A. | -5 | B. | -6 | C. | 5 | D. | 6 |
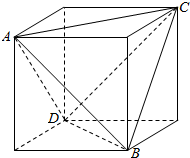 从一个正方体中,如图那样截去4个三棱锥后,得到一个正三棱锥A-BCD(底面是正三角形,各侧面是全等的等腰三角形的三棱锥叫做正三棱锥),问它的体积是正方体体积的几分之几?
从一个正方体中,如图那样截去4个三棱锥后,得到一个正三棱锥A-BCD(底面是正三角形,各侧面是全等的等腰三角形的三棱锥叫做正三棱锥),问它的体积是正方体体积的几分之几?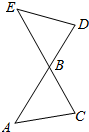 如图所示,某公园计划用鹅卵石铺成两条交叉的“健康石道”(线段AD和CE),并在这两条“健康石道”两端之间建设“花卉长廊”(线段AC和ED),以供市民休闲健身.已铺设好的部分BD=20m,ED=10$\sqrt{6}$m,∠BED=45°(△BDE为锐角三角形).由于设计要求,未铺设好的部分AB和BC的总长只能为40m,则剩余的“花卉长廊”(线段AC)最短可以是20m.
如图所示,某公园计划用鹅卵石铺成两条交叉的“健康石道”(线段AD和CE),并在这两条“健康石道”两端之间建设“花卉长廊”(线段AC和ED),以供市民休闲健身.已铺设好的部分BD=20m,ED=10$\sqrt{6}$m,∠BED=45°(△BDE为锐角三角形).由于设计要求,未铺设好的部分AB和BC的总长只能为40m,则剩余的“花卉长廊”(线段AC)最短可以是20m.