题目内容
14. 如图,直三棱柱ABC-A1B1C1的底面为等边三角形,侧面AA1C1C是正方形,E是A1B的中点,F是棱CC1上的点.
如图,直三棱柱ABC-A1B1C1的底面为等边三角形,侧面AA1C1C是正方形,E是A1B的中点,F是棱CC1上的点.(1)若F是CC1的中点,求证:AE⊥平面A1FB;
(2)当VB-AEF=9$\sqrt{3}$时,求正方形AA1C1C的边长.
分析 (1)取AB的中点为M,连接EF,EM,CM,由已知条件推导出四边形EMCF是平行四边形,由AE⊥A1B,AE⊥A1B,能证明AE⊥平面A1FB.
(2)设正方形AA1C1C的边长为x,由已知条件推导出点F到平面EAB的距离即为点C到平面平面AA1B的距离,由VE-EABF=VF-ABE,利用等积法能求出正方形的边长.
解答 解:(1)取AB的中点M,连接EM,CM,
如图所示: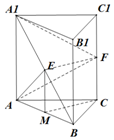 ,
,
∵E是A1B的中点,F是棱CC1的中点,
∴$EM∥A{A_1},FC∥A{A_1},EM=FC=\frac{1}{2}A{A_1}$,
则四边形EMCF是平行四边形,
∴EF∥CM,
又△ABC为等边三角形,侧面AA1C1C是正方形,
∴AA1=AB,AE⊥A1B,CM⊥AB,
∵侧棱AA1⊥平面ABC,∴CM⊥AA1,
∴CM⊥平面A1AB,∴EF⊥平面A1AB,
∴EF⊥AE,
又AE⊥A1B,A1B∩EF=E,
∴AE⊥平面A1FB;
(2)设正方形AA1C1C的边长为x,
∵CC1∥平面A1AB,
∴点F到平面EAB的距离即为点C到平面A1AB的距离h,
易知$h=\frac{{\sqrt{3}}}{2}x$,
$又{V_{B-AEF}}={V_{F-ABE}},且{V_{F-ABE}}=\frac{1}{3}{S_{△ABE}}•h=9\sqrt{3}$,
$即\frac{1}{3}×\frac{1}{2}×x×\frac{x}{2}×\frac{{\sqrt{3}}}{2}x=9\sqrt{3}$,
∴x3=216,x=6,
∴正方形AA1C1C的边长为6.
点评 本题考查直线与平面垂直的证明,考查正方形的边长的求法,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
4.由y=2cos2x的图象向右平移a个单位长度可以得到函数f(x)=2sin(3x+$\frac{π}{3}$)的图象,则a的最小值为( )
| A. | $\frac{π}{12}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{6}$ |
2.由曲线y=$\sqrt{2x}$,直线y=x-4及y轴所围成的封闭图形的面积为( )
| A. | $\frac{40}{3}$ | B. | $\frac{64}{3}$ | C. | 16$\sqrt{2}$ | D. | 32 |
9.已知集合A={x|$\frac{x-3}{x-2}$>0},B={x||x-1|≤2},则A∩B=( )
| A. | (-∞,-1)∪[2,3) | B. | [-1,2) | C. | (-∞,-1)∪[2,3)∪(3,+∞) | D. | (-∞,-1)∪(3,+∞) |
6.在直角坐标系中,若不等式组$\left\{\begin{array}{l}{y≥0}\\{y≤x}\\{y≤k(x-1)-1}\end{array}\right.$表示一个三角形区域,则实数k的取值范围是( )
| A. | (-∞,-1) | B. | (-1,2) | C. | (-∞,-1)∪(2,+∞) | D. | (2,+∞) |
 如图,在四棱锥P-ABCD中,底面ABCD是梯形,AD∥BC,∠DAB=90°,PA⊥平面ABCD,PA=AB=BC=2,AD=1.
如图,在四棱锥P-ABCD中,底面ABCD是梯形,AD∥BC,∠DAB=90°,PA⊥平面ABCD,PA=AB=BC=2,AD=1.