题目内容
2．由曲线y=$\sqrt{2x}$，直线y=x-4及y轴所围成的封闭图形的面积为（ ）| A． | $\frac{40}{3}$ | B． | $\frac{64}{3}$ | C． | 16$\sqrt{2}$ | D． | 32 |
分析 首先由题意求得交点坐标，然后结合定积分的几何意义求解定积分的数值即可求得面积．
解答 解：联立直线与曲线的方程：$\left\{\begin{array}{l}{y=\sqrt{2x}}\\{y=x-4}\end{array}\right.$ 可得交点坐标为（8，4），
结合定积分与几何图形面积的关系可得阴影部分的面积为：${∫}_{0}^{8}（\sqrt{2x}-x+4）dx=（\frac{2}{3}\sqrt{2}{x}^{\frac{3}{2}}-\frac{1}{2}{x}^{2}+4x）{|}_{0}^{8}=\frac{64}{3}$．
故选：B．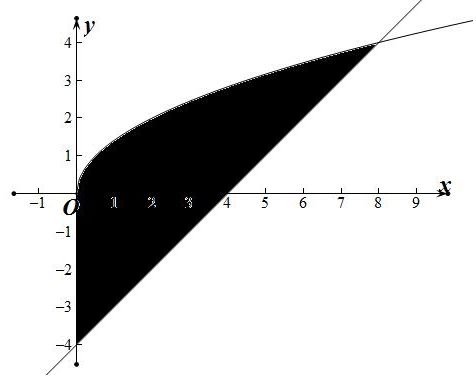
点评 本题考查定积分的几何意义及其运算，考查微积分基本定理和基本初等函数的导函数，属于基础题．
练习册系列答案
相关题目
13．已知x∈R，a=x2-1，b=2x+2，若用反证法证明结论“a，b中至少有一个不小于0”时，首先应假设（ ）
| A． | a≥0且b≥0 | B． | a≤0且b≤0 | C． | a＜0且b＜0 | D． | a＜0或b＜0 |
如图所示，在四棱锥P-ABCD中，AB⊥平面PAD，AB∥CD，PD=AD，E是PB的中点，F是CD上的点且DF=$\frac{1}{2}$AB，PH为△PAD中AD边上的高．
如图，直三棱柱ABC-A1B1C1的底面为等边三角形，侧面AA1C1C是正方形，E是A1B的中点，F是棱CC1上的点．
11．将函数y=cosx的图象向左平移N个单位（N＞0），得到的函数图象关于点（$\frac{π}{3}$，0）成中心对称，则N的最小值为（ ）
| A． | $\frac{π}{6}$ | B． | $\frac{π}{4}$ | C． | $\frac{π}{3}$ | D． | $\frac{π}{2}$ |