题目内容
在平面直角坐标系中,有三个点的坐标分别是A(-4,0),B(0,6),C(1,2).
(1)证明:A,B,C三点不共线;
(2)求过A,B的中点且与直线x+y-2=0平行的直线方程;
(3)设过C且与AB所在的直线垂直的直线为l,求l与两坐标轴围成的三角形的面积.
(1)证明:A,B,C三点不共线;
(2)求过A,B的中点且与直线x+y-2=0平行的直线方程;
(3)设过C且与AB所在的直线垂直的直线为l,求l与两坐标轴围成的三角形的面积.
考点:直线的截距式方程,直线的斜率
专题:直线与圆
分析:(1)只要证明kAB≠kAC,可得A,B,C三点不共线.
(2)利用中点坐标公式、相互平行的直线斜率之间的关系即可得出;
(3)利用相互垂直的直线斜率之间的关系、三角形的面积计算公式即可得出.
(2)利用中点坐标公式、相互平行的直线斜率之间的关系即可得出;
(3)利用相互垂直的直线斜率之间的关系、三角形的面积计算公式即可得出.
解答:
(1)证明:∵KAB=
=
,KAC=
=
,
∴kAB≠kAC.
∴A,B,C三点不共线.
(2)解:∵A,B的中点坐标为M(-2,3),
直线x+y-2=0的斜率k1=-1,
s∴满足条件的直线方程为y-3=-(x+2),
即x+y-1=0为所求.
(3)解:∵KAB=
,
∴与AB所在直线垂直的直线的斜率为k2=-
,
∴满足条件的直线l的方程为y-2=-
(x-1),即2x+3y-8=0.
∵直线l在x,y轴上的截距分别为4和
,
∴l与两坐标轴围成的三角形的面积为S=
×4×
=
.
| 6-0 |
| 0-(-4) |
| 3 |
| 2 |
| 2-0 |
| 1-(-4) |
| 2 |
| 5 |
∴kAB≠kAC.
∴A,B,C三点不共线.
(2)解:∵A,B的中点坐标为M(-2,3),
直线x+y-2=0的斜率k1=-1,
s∴满足条件的直线方程为y-3=-(x+2),
即x+y-1=0为所求.
(3)解:∵KAB=
| 3 |
| 2 |
∴与AB所在直线垂直的直线的斜率为k2=-
| 2 |
| 3 |
∴满足条件的直线l的方程为y-2=-
| 2 |
| 3 |
∵直线l在x,y轴上的截距分别为4和
| 8 |
| 3 |
∴l与两坐标轴围成的三角形的面积为S=
| 1 |
| 2 |
| 8 |
| 3 |
| 16 |
| 3 |
点评:本题考查了三点不共线与斜率之间的关系、中点坐标公式、相互平行的直线斜率之间的关系、相互垂直的直线斜率之间的关系、三角形的面积计算公式,考查了计算能力,属于基础题.

练习册系列答案
相关题目
执行如图所示的程序框图,输出的s值为( )
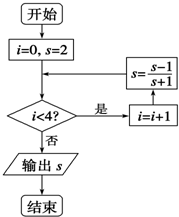

| A、-3 | ||
B、-
| ||
| C、2 | ||
D、
|