题目内容

设f(x)=
4x
4x+2
，求f(
1
1001
)+f(
2
1001
)+f(
3
1001
)+…+f(
1000
1001
)的值．
考点：函数的值
专题：函数的性质及应用
分析：观察题设，探索出f（x）+f（1-x）=1即可求解．
解答： 解：f（1-x）=
41-x
41-x+2
=
4
4+2•4x
=
2
2+4x
，
∴f（x）+f（1-x）=
4x
4x+2
+
2
2+4x
=1，
∴f(
1
1001
)+f(
1000
1001
)=f(
2
1001
)+f(
999
1001
)=…=f（
500
1001
）=f（
501
1001
）=1，
∴f(
1
1001
)+f(
2
1001
)+f(
3
1001
)+…+f(
1000
1001
)=500．
点评：本题考查函数的求值，解决本题的关键是观察题设，寻求规律．
练习册系列答案
相关题目
已知扇形的面积等于
π
6
cm2，弧长为 
π
3
cm，则圆心角等于（　　）
A、
π
6
B、
π
4
C、
π
3
D、
π
2
已知数列{xn}，{yn}满足：x1=x2=1，y1=y2=2，并且
xn+1
xn
=λ•
xn
xn-1
，
yn+1
yn
≥λ•
yn
yn-1
（λ为非零参数，n=2，3，4…）
（1）若x1，x3，x5成等比数列，求参数λ的值；
（2）当λ＞0时，证明：
xn+1
yn+1
≤
xn
yn
(n∈N*)；
（3）当λ＞1时，证明：
x1-y1
x2-y2
+
x2-y2
x3-y3
+…+
xn-yn
xn+1-yn+1
＜
λ
λ-1
．
一个几何体的三视图如图所示（单位：m），则该几何体的体积为（　　）
A、9+πB、6+π
C、6+3πD、9+3π
某工程队有5项工程需要单独完成，其中工程乙必须在工程甲完成后才能进行，工程丙必须在工程乙完成后立即进 行那么安排这5项工程的不同排法种数是
 
．（用数字作答）
已知定点A（2，0），点P（x，y）的坐标满足
x-4y+3≤0
3x+5y-25≤0
x-a≥0
，当
OP
•
OA
|
OA
|
（O为坐标原点）的最小值是2时，实数a的值是
 
．
已知两圆的半径分别为7和1，当它们内切时，圆心距为（　　）
A、6B、7C、8D、9
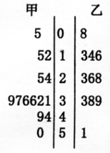如图为甲、乙两名篮球运动员每场比赛的得分情况的茎叶图，则甲运动员的得分的中位数是
 
．
函数y=10x与函数y=x+2的图象的交点个数为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网