题目内容
已知点O（0，0），A（1，2）动点P满足|
+
|=2，则点P的轨迹方程是（ ）
| OP |
| AP |
| A、4x2+4y2-4x-8y+1=0 |
| B、4x2+4y2-4x-8y-1=0 |
| C、8x2+8y2+2x+4y-5=0 |
| D、8x2+8y2-2x+4y-5=0 |
考点：轨迹方程
专题：平面向量及应用,直线与圆
分析：设出P的坐标，得到两个向量
，
的坐标，求出两向量坐标的和，代入|
+
|=2整理得答案．
| OP |
| AP |
| OP |
| AP |
解答：
解：设P（x，y），
由O（0，0），A（1，2），得
=(x，y)，
=(x-1，y-2)，
+
=(2x-1，2y-2)，
由|
+
|=2，得
=2，
整理得：4x2+4y2-4x-8y+1=0．
故选：A．
由O（0，0），A（1，2），得
| OP |
| AP |
| OP |
| AP |
由|
| OP |
| AP |
| (2x-1)2+(2y-2)2 |
整理得：4x2+4y2-4x-8y+1=0．
故选：A．
点评：本题考查了轨迹方程的求法，考查了平面向量的坐标运算，考查了向量的模，是中档题．
练习册系列答案
相关题目
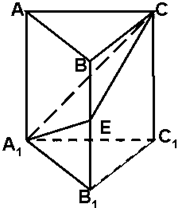在三棱柱ABC-A1B1C1中，底面为等边三角形且侧棱与底面垂直，E是棱BB1上的点，AB=AA1，且平面A1EC⊥平面AA1C1C．