题目内容
12.设函数$f(x)=sin(2x+\frac{π}{3})+\sqrt{3}-2\sqrt{3}{cos^2}$x+1(1)求f(x)的最小正周期及其图象的对称中心;
(2)求函数f(x)的单调递增区间.
分析 (1)利用三角恒等变换化简函数的解析式,再利用正弦函数的周期性以及它的图象的对称性,求得f(x)的最小正周期及其图象的对称中心.
(2)利用正弦函数的单调性,求得函数f(x)的单调递增区间.
解答 解:(1)f(x)=$\frac{1}{2}$sin2x+$\frac{\sqrt{3}}{2}$cos2x-$\sqrt{3}$cos2x+1=$\frac{1}{2}$sin2x-$\frac{\sqrt{3}}{2}$cos2x+1=sin(2x-$\frac{π}{3}$)+1,
所以f(x)的最小正周期为T=$\frac{2π}{2}$=π.
令2x-$\frac{π}{3}$=kπ(k∈Z),求得x=$\frac{kπ}{2}$+$\frac{π}{6}$,可得函数的图象对称中心为($\frac{kπ}{2}$+$\frac{π}{6}$,1)(k∈Z).
(2)令2kπ-$\frac{π}{2}$≤2x-$\frac{π}{3}$≤2kπ+$\frac{π}{2}$(k∈Z),解得kπ-$\frac{π}{12}$≤x≤kπ+$\frac{5π}{12}$(k∈Z),
所以f(x)的单调递增区间为[kπ-$\frac{π}{12}$,kπ+$\frac{5π}{12}$](k∈Z).
点评 本题主要考查三角恒等变换,正弦函数的周期性和单调性,以及它的图象的对称性,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.设x、y满足不等式组$\left\{\begin{array}{l}{x-2y+1≤0}\\{2x+y-6≤0}\\{x-y+a≥0}\end{array}\right.$,其中a为常数,当且仅当x=y=1时,目标函数z=x+2y取得最小值,则目标函数z的最大值为( )
| A. | 8 | B. | $\frac{27}{5}$ | C. | 6 | D. | 3 |
20.若函数f(x)与函数g(x)的奇偶性相同,则称g(x)为f(x)的同心函数.那么,在下列给出的函数中,为函数f(x)=$\frac{{{x^2}-1}}{x}$的同心函数的是( )
| A. | g(x)=x+1 | B. | g(x)=2x | C. | g(x)=x2 | D. | g(x)=lnx |
7.如图给出了计算S=$\frac{1}{2}$+$\frac{1}{4}$+…+$\frac{1}{60}$的值的程序框图,其中 ①②分别是( )
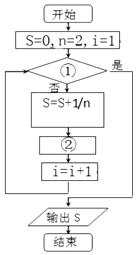

| A. | i<30,n=n+2 | B. | i>30,n=n+2 | C. | i<30,n=n+1 | D. | i>30,n=n+1 |
17.设集合A={x|-1<x<2},B={x|y=lg(x-1)},则A∩(∁RB)=( )
| A. | [-1,2) | B. | [2,+∞) | C. | (-1,1] | D. | [-1,+∞) |
2.若$\overrightarrow{a}$=(1,3),$\overrightarrow{b}$=(-2,4)则$\overrightarrow{a}$在$\overrightarrow{b}$方向上的投影是( )
| A. | $\sqrt{10}$ | B. | $\sqrt{10}$ | C. | $\sqrt{5}$ | D. | -$\sqrt{5}$ |
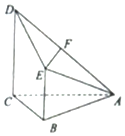 已知四棱锥A-BCDE中,侧面△ABC为等边三角形,BE=AB,CD=2AB,CD∥BE,且CD⊥平面ABC,F为棱AD的中点.
已知四棱锥A-BCDE中,侧面△ABC为等边三角形,BE=AB,CD=2AB,CD∥BE,且CD⊥平面ABC,F为棱AD的中点.