题目内容
13.在△ABC中的内角A,B,C所对的边长分别为a,b,c,若$\sqrt{5}$b=4c,B=2C.(1)求cosB;
(2)若c=5,点D为BC上一点,且BD=6,求△ADC的面积.
分析 (1)由B=2C,推导出cosC=$\frac{sinB}{2sinC}$=$\frac{b}{2c}$=$\frac{2\sqrt{5}}{5}$,由此能求出cosB.
(2)由题意得,b=4$\sqrt{5}$,由余弦定理得a=11,从嘏求出DC=5,sinC=$\frac{\sqrt{5}}{5}$,由此能求出△ADC的面积.
解答 解:(1)因为B=2C,所以有sinB=sin2C=2sinCcosC.
从而cosC=$\frac{sinB}{2sinC}$=$\frac{b}{2c}$=$\frac{2\sqrt{5}}{5}$.
故cosB=cos2C=2cos2C-1=$\frac{8}{5}-1$=$\frac{3}{5}$.
(2)由题意得,b=4$\sqrt{5}$,
由余弦定理得,b2=a2+c2-2accosB.
即80=${a}^{2}+{5}^{2}-2×5×\frac{3}{5}a$,化简得a2-6a-55=0,
解得a=11或a=-5(舍去).
从而DC=5,又cosC=$\frac{2\sqrt{5}}{5}$,则sinC=$\sqrt{1-(\frac{2\sqrt{5}}{5})^{2}}$=$\frac{\sqrt{5}}{5}$.
所以△ADC的面积${S}_{△ADC}=\frac{1}{2}×DC×AC×sinC$=10.
点评 本题考查三角形内角的余弦值、三角形面积、余弦定理、同角三角函数关系式等基础知识,考查推理论证能力、运算求解能力,考查数形结合思想、化归与转化思想,考查创新意识、应用意识,是中档题.

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目
3.设x、y满足不等式组$\left\{\begin{array}{l}{x-2y+1≤0}\\{2x+y-6≤0}\\{x-y+a≥0}\end{array}\right.$,其中a为常数,当且仅当x=y=1时,目标函数z=x+2y取得最小值,则目标函数z的最大值为( )
| A. | 8 | B. | $\frac{27}{5}$ | C. | 6 | D. | 3 |
2.若$\overrightarrow{a}$=(1,3),$\overrightarrow{b}$=(-2,4)则$\overrightarrow{a}$在$\overrightarrow{b}$方向上的投影是( )
| A. | $\sqrt{10}$ | B. | $\sqrt{10}$ | C. | $\sqrt{5}$ | D. | -$\sqrt{5}$ |
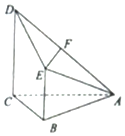 已知四棱锥A-BCDE中,侧面△ABC为等边三角形,BE=AB,CD=2AB,CD∥BE,且CD⊥平面ABC,F为棱AD的中点.
已知四棱锥A-BCDE中,侧面△ABC为等边三角形,BE=AB,CD=2AB,CD∥BE,且CD⊥平面ABC,F为棱AD的中点.