题目内容

函数y=loga（x-2）+1（a＞0且a≠1）的图象恒过的一个定点是（　　）
A、（3，0）
B、（3，1）
C、（2，1）
D、（2，2）
考点：对数函数的单调性与特殊点
专题：函数的性质及应用
分析：令对数的真数等于1，求得x、y的值，可得函数图象经过的定点的坐标．
解答： 解：令x-2=1，求得 x=3，y=1，
故函数y=loga（x-2）+1（a＞0且a≠1）的图象恒过的一个定点（3，1），
故选：B．
点评：本题主要考查对数函数的单调性和特殊点，属于基础题．
练习册系列答案
相关题目
设f（x）=xex，g（x）=-（x+1）2+a，若?x1，x2∈R，使得g（x2）≤f（x1）成立，则实数a的取值范围是
 
．
若正三棱锥的底面边长为a，侧面积为
3
a2，则它的体积是
 
．
已知不重合的两条直线l，m和不重合的两个平面α，β，下列命题正确的是（　　）
A、l∥m，l∥β，则m∥β
B、α∩β=m，l?α，则l∥β
C、α⊥β，l⊥α，则l∥β
D、l⊥m，m⊥β，l⊥α，则α⊥β
已知函数f（x）=sin2ωx+
3
sinωxsin（ωx+
π
2
），（ω＞0）的最小正周期为π，则f（x）在区间[0，
2π
3
]上的值域为（　　）
A、[0，
3
2
]
B、[-
1
2
，
3
2
]
C、[-
1
2
，1]
D、[-
3
2
，
1
2
]
设数列{an}是等比数列，满足an＞0，q＞1，且a3+a5=20，a2•a6=64，则a6=（　　）
A、16B、32C、42D、48
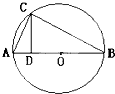如图，圆的直径AB=13cm，C为圆上的一点，CD⊥AB，垂足为D，且CD=6cm，则AD的长是（　　）
A、4B、9C、4或9D、6
下面是关于复数z=
2
-1+i
的四个命题：
P1：|z|=2        
P2：z2=2i      
P3：z的共轭复数为1+i       
P4：z的虚部为-1
其中真命题为（　　）
A、P2，P3
B、P1，P2
C、P2，P4
D、P3，P4
在极坐标系中，圆ρ=2cosθ+2sinθ的圆心的极坐标是（　　）
A、（1，
π
2
）
B、（1，
π
4
）
C、（
2
，
π
4
）
D、（
2
，
π
2
）

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网