题目内容
已知直线L:x=my+n(n>0)过点A(5
,5),若可行域的面积
为25
,则(n+mx)4展开式中系数绝对值得和为( )
| 3 |
|
| 3 |
A、(11
| ||
| B、9×114 | ||
| C、9×104 | ||
| D、9×115 |
考点:简单线性规划
专题:不等式的解法及应用,二项式定理
分析:根据条件确定n,m的值,利用二项式的性质令x=-1,即可得到结论
解答:
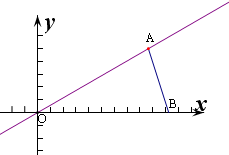 解:∵x=my+n(n>0)过点A(5
解:∵x=my+n(n>0)过点A(5
,5),
∴5
=5m+n,
则直线x-
y=0也过点A,
作出不等式组对应的平面区域如图,
设B(a,0),
则三角形OAB的面积为
a×5=25
,
解得a=10
,则B(10
,0)也在x=my+n上,
∴10
=n,则m=-
,
则二项式为(10
-
x)4,
令x=-1,可得(10
-
x)4的展开式中系数绝对值和为
(10
+
)4=(11
)4,
故选:A
 解:∵x=my+n(n>0)过点A(5
解:∵x=my+n(n>0)过点A(5| 3 |
∴5
| 3 |
则直线x-
| 3 |
作出不等式组对应的平面区域如图,
设B(a,0),
则三角形OAB的面积为
| 1 |
| 2 |
| 3 |
解得a=10
| 3 |
| 3 |
∴10
| 3 |
| 3 |
则二项式为(10
| 3 |
| 3 |
令x=-1,可得(10
| 3 |
| 3 |
(10
| 3 |
| 3 |
| 3 |
故选:A
点评:本题主要考查线性规划的应用以及二项式定理,根据条件求出,m,n的值是解决本题的关键.

练习册系列答案
相关题目
已知函数f(x)=sin2ωx+
sinωxsin(ωx+
),(ω>0)的最小正周期为π,则f(x)在区间[0,
]上的值域为( )
| 3 |
| π |
| 2 |
| 2π |
| 3 |
A、[0,
| ||||
B、[-
| ||||
C、[-
| ||||
D、[-
|
在等差数列{an}中,若a3+a7=10,则等差数列{an}的前9项和S9等于( )
| A、45 | B、48 | C、54 | D、108 |
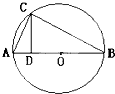 如图,圆的直径AB=13cm,C为圆上的一点,CD⊥AB,垂足为D,且CD=6cm,则AD的长是( )
如图,圆的直径AB=13cm,C为圆上的一点,CD⊥AB,垂足为D,且CD=6cm,则AD的长是( )| A、4 | B、9 | C、4或9 | D、6 |
已知复数z=
,则( )
| 2 |
| -1+i |
| A、z的虚部为-1 |
| B、z的实部为1 |
| C、|z|=2 |
| D、z的共轭复数为1+i |
已知点P的极坐标是(2,
),则过点P且平行极轴的直线方程是( )
| π |
| 6 |
| A、ρ=1 | ||
| B、ρ=sinθ | ||
C、ρ=-
| ||
D、ρ=
|
已知点P(-1,1)与点Q(3,5)关于直线l对称,则直线l的方程为( )
| A、x-y+1=0 |
| B、x+y=0 |
| C、x+y-4=0 |
| D、x-y=0 |