题目内容
6.在△ABC中,($\frac{\overrightarrow{AB}}{|\overrightarrow{AB}|}$+$\frac{\overrightarrow{AC}}{|\overrightarrow{AC}|}$)•($\overrightarrow{AC}$+$\overrightarrow{BA}$)=0,|$\overrightarrow{AB}$+$\overrightarrow{AC}$|=3,A∈[$\frac{π}{3}$,$\frac{5π}{6}$],则$\overrightarrow{AB}$•$\overrightarrow{AC}$的最大值是$\frac{9}{8}$.分析 根据题意,得出$\overrightarrow{AD}$⊥$\overrightarrow{BC}$,且AD平分∠BAC;又|$\overrightarrow{AB}$+$\overrightarrow{AC}$|=3,A∈[$\frac{π}{3}$,$\frac{5π}{6}$],
再利用数量积的定义与基本不等式求出$\overrightarrow{AB}$•$\overrightarrow{AC}$的最大值.
解答 解:△ABC中,($\frac{\overrightarrow{AB}}{|\overrightarrow{AB}|}$+$\frac{\overrightarrow{AC}}{|\overrightarrow{AC}|}$)•($\overrightarrow{AC}$+$\overrightarrow{BA}$)=0,
∴($\frac{\overrightarrow{AB}}{|\overrightarrow{AB}|}$+$\frac{\overrightarrow{AC}}{|\overrightarrow{AC}|}$)•$\overrightarrow{BC}$=0,
∴$\overrightarrow{AD}$⊥$\overrightarrow{BC}$,且AD平分∠BAC;
又|$\overrightarrow{AB}$+$\overrightarrow{AC}$|=3,
∴|$\overrightarrow{AD}$|=$\frac{3}{2}$,如图所示;
又A∈[$\frac{π}{3}$,$\frac{5π}{6}$],
$\overrightarrow{AB}$•$\overrightarrow{AC}$的最大值是|$\overrightarrow{AB}$|•|$\overrightarrow{AC}$|cos$\frac{π}{3}$=$\frac{1}{2}$|$\overrightarrow{AB}$||$\overrightarrow{AC}$|≤$\frac{1}{2}$×$\frac{1}{4}$${(\overrightarrow{AB}+\overrightarrow{AC})}^{2}$=$\frac{9}{8}$.
故答案为:$\frac{9}{8}$.
点评 本题考查了平面向量的应用问题,也考查了数量积与基本不等式的应用问题,是综合性题目.

| A. | f(x)=cos$\frac{πx}{3}$ | B. | $f(x)=sin\frac{πx}{3}$ | C. | f(x)=2cos2$\frac{πx}{6}$ | D. | f(x)=2cos2$\frac{πx}{12}$ |
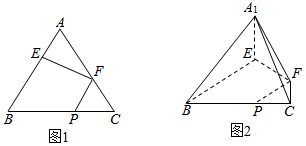 在正三角形ABC中,E,F,P分别是AB,AC,BC边上的点满足AE:EB=CF:FA=CP:PB=1:2(如图1),将△AEF折起到△A1EF的位置上,连接A1B,A1C(如图2)
在正三角形ABC中,E,F,P分别是AB,AC,BC边上的点满足AE:EB=CF:FA=CP:PB=1:2(如图1),将△AEF折起到△A1EF的位置上,连接A1B,A1C(如图2)