题目内容
2.设函数y=f(x)是定义在R上的偶函数,对任意的x∈R都有f(x+6)=f(x)+f(3),则满足上述条件的f(x)可以是( )| A. | f(x)=cos$\frac{πx}{3}$ | B. | $f(x)=sin\frac{πx}{3}$ | C. | f(x)=2cos2$\frac{πx}{6}$ | D. | f(x)=2cos2$\frac{πx}{12}$ |
分析 根据抽象函数关系结合函数奇偶性的性质求出f(3)=0,从而得到函数的周期是6,结合三角函数的周期性进行判断即可.
解答 解:∵f(x+6)=f(x)+f(3),
∴f(-3+6)=f(-3)+f(3),
∴f(-3)=0,函数f(x)是偶函数,
∴f(3)=0.
∴f(x+6)=f(x)+0=f(x),
∴f(x)是以6为周期的函数,
A.函数的周期T=$\frac{2π}{\frac{1}{3}π}$=6,f(3)=cosπ=-1,不满足条件f(3)=0.
B.$f(x)=sin\frac{πx}{3}$是奇函数,不满足条件.
C.f(x)=2cos2$\frac{πx}{6}$=1+cos$\frac{πx}{3}$,则函数的周期是T=$\frac{2π}{\frac{1}{3}π}$=6,f(3)=1+cosπ=1-1=0,满足条件.
D.f(x)=2cos2$\frac{πx}{12}$=1+cos$\frac{πx}{6}$,则函数的周期是T=$\frac{2π}{\frac{π}{6}}$=12,不满足条件.
故选:C.
点评 本题主要考查抽象函数的应用,根据函数的奇偶性得到函数的周期性,结合三角函数的周期性是解决本题的关键.

练习册系列答案
相关题目
10.7人站成两排队列,前排3人,后排4人,现将甲、乙、丙三人加入队列,前排加一人,后排加两人,其他人保持相对位置不变,则不同的加入方法种数为( )
| A. | 120 | B. | 240 | C. | 360 | D. | 480 |
7.A,B分别是y=kx和$y=-\frac{1}{k}x$与椭圆$\frac{x^2}{2}+{y^2}=1$的交点,点P在线段AB上,且$\overrightarrow{OA}•\overrightarrow{OP}=\overrightarrow{OB}•\overrightarrow{OP}$,当k变化时,点P一定在( )
| A. | 双曲线x2-2y2=1上 | B. | 椭圆${x^2}+\frac{y^2}{2}=1$上 | ||
| C. | 圆${x^2}+{y^2}=\frac{1}{3}$上 | D. | 圆${x^2}+{y^2}=\frac{2}{3}$上 |
14.若tan(π+α)=3,则sin(-α)cos(π-α)=( )
| A. | $-\frac{3}{10}$ | B. | $\frac{3}{10}$ | C. | $-\frac{1}{10}$ | D. | $\frac{1}{10}$ |
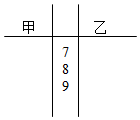 甲乙两组数学兴趣小组的同学举行了赛前模拟考试,成绩记录如下(单位:分):
甲乙两组数学兴趣小组的同学举行了赛前模拟考试,成绩记录如下(单位:分):