题目内容
2.求函数y=3x2-6x-9在[-1,1]上的最大值和最小值.分析 求得二次函数的对称轴,可得区间[-1,1]为递减,可得最值.
解答 解:函数y=3x2-6x-9=3(x-1)2-12,
对称轴为x=1,
即有函数在[-1,1]上递减,
可得f(x)的最大值为f(-1)=0;
f(x)的最小值为f(1)=-12.
点评 本题考查二次函数的最值的求法,注意运用对称轴和区间的关系,考查运算能力,属于基础题.

练习册系列答案
相关题目
14.若z=$\frac{3+2i}{i}$,则|$\overline{z}$-1|等于( )
| A. | 3 | B. | 5 | C. | $\sqrt{10}$ | D. | $\sqrt{13}$ |
11.设函数f(x)=sin$\frac{π}{6}$x,则f(1)+f(2)+f(3)+…+f(2009)的值等于( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{1+\sqrt{3}}{2}$ | D. | 2+$\sqrt{3}$ |
14.命题“?x0∈R,x0+1<0或x02-x0>0”的否定形式是( )
| A. | ?x0∈R,x0+1≥0或$x_0^2-{x_0}≤0$ | B. | ?x∈R,x+1≥0或x2-x≤0 | ||
| C. | ?x0∈R,x0+1≥0且$x_0^2-{x_0}≤0$ | D. | ?x∈R,x+1≥0且x2-x≤0 |
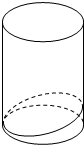 如图,用与圆柱的母线成60°角的平面截圆柱得到的截口曲线是椭圆,则该椭圆的离心率为$\frac{1}{2}$.
如图,用与圆柱的母线成60°角的平面截圆柱得到的截口曲线是椭圆,则该椭圆的离心率为$\frac{1}{2}$.