题目内容
函数f(x)对于任意实数x满足条件f(x+2)f(x)=1,若f(1)=-5,则f(-5)= .
考点:函数的值
专题:函数的性质及应用
分析:根据函数的周期性
解答:
解:∵f(x+2)f(x)=1,
∴f(x)≠0,且f(x+4)f(x+2)=f(x+2)f(x),
即f(x+4)=f(x),即函数的周期是4,
故f(-5)=f(-1)=
=-
,
故答案为为:-
∴f(x)≠0,且f(x+4)f(x+2)=f(x+2)f(x),
即f(x+4)=f(x),即函数的周期是4,
故f(-5)=f(-1)=
| 1 |
| f(1) |
| 1 |
| 5 |
故答案为为:-
| 1 |
| 5 |
点评:本题主要考查函数值的计算,根据条件得到函数的周期性是解决本题的关键.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案
相关题目
下列说法错误的是( )
| A、如果命题“¬p”与命题“p∨q”都是真命题,那么命题q一定是真命题 | ||
| B、命题“若a=0,则ab=0”的否命题是:“若a≠0,则ab≠0” | ||
| C、若命题p:?x0∈R,x02+2x0-3<0,则?p:?x∈R,x2+2x-3≥0 | ||
D、“sinθ=
|
已知直线y=b(b>0)与曲线f(x)=sinx在y轴右侧依次的三个交点的横坐标x1,x2,x3成等比数列,则b的值为( )
A、
| ||||
B、
| ||||
C、
| ||||
| D、1 |
已知y=f(x)在R上可导,且f(1)=2,若f′(x)>2,则不等式f(x)>2x的解集为( )
| A、(-∞,1) |
| B、(1,+∞) |
| C、(-∞,0) |
| D、(0,+∞) |
 把正整数按一定的规则排成了如图所示的三角形数表.设aij(i,j∈N+)是位于这个三角形数表中从上往下数第i行、从左往右数第j个数,如a42=8.若aij=2014,则i+j=
把正整数按一定的规则排成了如图所示的三角形数表.设aij(i,j∈N+)是位于这个三角形数表中从上往下数第i行、从左往右数第j个数,如a42=8.若aij=2014,则i+j=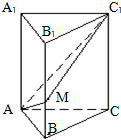 如图,直三棱柱ABC-A1B1C1中,AB=1,BC=2,AC=
如图,直三棱柱ABC-A1B1C1中,AB=1,BC=2,AC=