题目内容
14.定义在R上的函数f(x)满足f(x)=$\left\{\begin{array}{l}{x^2}-{2^x},x≤0\\ f(x-1)-f(x-2),x>0\end{array}$,则f(2016)的值为-1.分析 由f(x)=f(x-1)-f(x-2)推导可得f(x)=-f(x-3)=f(x-6),从而解得.
解答 解:∵x>0,f(x)=f(x-1)-f(x-2)
=f(x-2)-f(x-3)-f(x-2)=-f(x-3),
∴f(x)=-f(x-3)=f(x-6),
故f(2016)=f(336•6)=f(0)=0-1=-1,
故答案为:-1.
点评 本题考查了学生的化简运算能力及函数的性质的判断与应用.

练习册系列答案
相关题目
4.如图是用同样规格的黑、白两色正方形瓷砖铺设的若干图案,则按此规律第n个图案中需用黑色瓷砖块数为( )
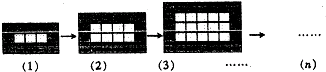

| A. | 4n+2 | B. | 4n+4 | C. | 4n+6 | D. | 4n+8 |
5.设正数数列{an}的前n项和为bn,数列{bn}的前n项之积为cn,且bn+cn=1,则数列{$\sqrt{\frac{1}{{a}_{n}}}$}的前n项和Sn中大于2016的最小项为第63项.
2.设数列{an}是公差不为零的等差数列,且a1,a3,a7构成等比数列,则公比q为( )
| A. | $\sqrt{2}$ | B. | 4 | C. | 2 | D. | $\frac{1}{2}$ |
9.若函数f(x)=2x2+(x-2a)|x-a|在区间[-3,1]上不是单调函数,则实数a的取值范围是( )
| A. | [-4,1] | B. | [-3,1] | C. | (-6,2) | D. | (-6,1) |
6.集合A={-2,-1,0,1,3},集合B={x|x>$\frac{1}{2}$ },则集合A∩(∁RB ) 等于( )
| A. | {1,3} | B. | {-2,-1} | C. | {-2,-1,0} | D. | {0,1,3} |